Chứng minh biểu thức: A= -3x2-6x-4< 0 với mọi x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) x2-6x+10
=(x^2-6x+9)+1
=(x-3)^2+1
vì (x-3)^2>=0 với mọi x nên (x-3)^2+1>0
Hay x^2-6x+10>0

b: \(=\left(x-5\right)^2-9y^2\)
\(=\left(x-5-3y\right)\left(x-5+3y\right)\)

Bài 1:
b: \(=\left(x-5\right)^2-9y^2\)
\(=\left(x-5-3y\right)\left(x-5+3y\right)\)

\(1,\\ a,=3x\left(x-3y\right)\\ b,=\left(x-5\right)^2-9y^2=\left(x-3y-5\right)\left(x+3y-5\right)\\ c,=3x\left(x-y\right)-2\left(x-y\right)=\left(3x-2\right)\left(x-y\right)\\ 2,\\ Sửa:x^2-6x+10=\left(x-3\right)^2+1\ge1>0,\forall x\)
1, =3x (2x -3y)
c, = 3x(x-y) -2(x-y)
= (3x-2)(x-y)
2, Ta có: x2 -6x+10= (x-3)2 +11
Nhận xét: (x-3)2 >= 0 với mọi số thực x
=> (x-3)2 +1 >= 1 >0 (đpcm)

Điều kiện x ≠ 0 và x ≠ -3
Ta có:
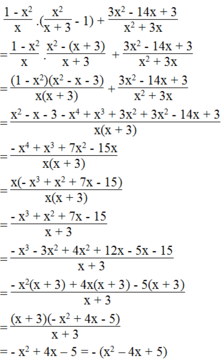
Vì x 2 - 4 x + 5 = x 2 - 4 x + 4 + 1 = x - 2 2 + 1 > 0 với mọi giá trị của x nên
- x 2 + 4 x - 5 = - x - 2 2 + 1 < 0 với mọi giá trị của x.
Vậy giá trị biểu thức luôn luôn âm với mọi giá trị x ≠ 0 và x ≠ -3

a) \(9x^2-6x+11=\left(3x\right)^2-2.3x+1+10=\left(3x-1\right)^2+10>0\forall x\)
b) \(3x^2-12x+81=3.\left(x^2-4x+9\right)=3.\left(x-2\right)^2+15>0\forall x\)
c) \(5x^2-5x+4=5.\left(x^2-x+\dfrac{4}{5}\right)=5.\left(x^2-x+\dfrac{1}{4}+\dfrac{11}{20}\right)=5.\left(x-\dfrac{1}{2}\right)^2+\dfrac{11}{4}>0\forall x\)
d) \(2x^2-2x+9=2.\left(x^2-x+\dfrac{9}{2}\right)=2.\left(x-\dfrac{1}{2}\right)^2+\dfrac{17}{2}>0\forall x\)