Giúp tôi giải bài này pls 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Để phương trình có hai nghiệm trái dấu thì 2m+1<0
hay m<-1/2
b: Để phương trình có hai nghiệm phân biệt thì 36-4(2m+1)>0
=>36-8m-4>0
=>-8m+32>0
=>-8m>-32
hay m<4
c: Để phương trình có hai nghiệm phân biệt cùng dấu thì \(\left\{{}\begin{matrix}m< 4\\2m+1>0\end{matrix}\right.\Leftrightarrow-\dfrac{1}{2}< m< 4\)


Bài 2:
a) Ta có: \(\text{Δ}=\left(m+1\right)^2-4\left(m-5\right)\)
\(=m^2+2m+1-4m+20\)
\(=m^2-2m+1+20\)
\(=\left(m-1\right)^2+20>0\forall m\)
Do đó: Phương trình luôn có hai nghiệm phân biệt với mọi m

câu 1: quan hệ từ vì biểu thị quan hệ nguyên nhân
câu 3: quan hệ từ và chỉ quan hệ song song
câu 4: cặp quan hệ từ nếu như...thì chỉ quan hệ điều kiện-kết quả


Lời giải:
Nếu $x+y+z+t=0$ thì $M=\frac{-t}{t}=\frac{-x}{x}=\frac{-z}{z}=-1$
$\Rightarrow (M-1)^{2025}=(-1-1)^{2025}=(-2)^{2025}$
Nếu $x+y+z+t\neq 0$. Áp dụng TCDTSBN:
$M=\frac{x+y+z}{t}=\frac{y+z+t}{x}=\frac{z+t+x}{y}=\frac{t+x+y}{z}=\frac{x+y+z+y+z+t+z+t+x+t+x+y}{t+x+y+z}=\frac{3(x+y+z+t)}{x+y+z+t}=3$
$\Rightarrow (M-1)^{2025}=2^{2025}$


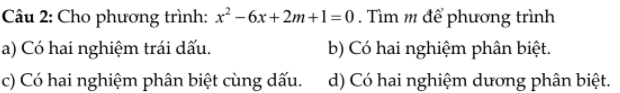


 Đây nè ae
Đây nè ae 



\(AE=2\times3=6\left(cm\right)\)
\(AD=2\times4=8\left(cm\right)\)
\(BE=BF=CF=2\times2=4\left(cm\right)\)
\(CD=2\times5=10\left(cm\right)\)
\(S_{ABCD}=AD\times CD=8\times10=80\left(cm^2\right)\)
\(S_{AED}=\frac{1}{2}\times6\times8=24\left(cm^2\right)\)
\(S_{BEF}=\frac{1}{2}\times4\times4=8\left(cm^2\right)\)
\(S_{FCD}=\frac{1}{2}\times4\times10=20\left(cm^2\right)\)
\(S_{DEF}=S_{ABCD}-S_{AED}-S_{BEF}-S_{FCD}=80-24-8-20=28\left(cm^2\right)\)