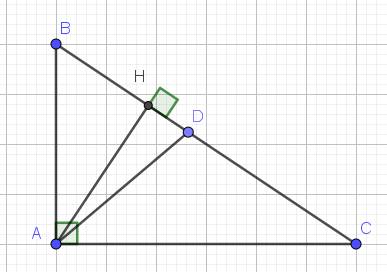
 = 90° , AB = 12cm , AC = 16cm Kẽ đường cao AH ( H € BC ) Tia phân giác góc A cắt BC tại D A) Chứng minh tam giác HBA đồng dạng tam giác ABC và AB²= BH . BC B) Tính độ dài BC , BD và CD C) Tính tỉ số điện tích tam giác ABD và tam giác ACD D) Từ D kẽ DE vuông với AC ( E € AC ) Tính độ dài đoạn DE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
27 tháng 1
Đúng(0)
Những câu hỏi liên quan
27 tháng 1
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{HBA}\) chung
Do đó;ΔHBA~ΔABC
=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}\)
=>\(BA^2=BH\cdot BC\)
b: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=12^2+16^2=400\)
=>\(BC=\sqrt{400}=20\left(cm\right)\)
Xét ΔABC có AD là phân giác
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
=>\(\dfrac{BD}{12}=\dfrac{CD}{16}\)
=>\(\dfrac{BD}{3}=\dfrac{CD}{4}\)
mà BD+CD=BC=20cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{20}{7}\)
=>\(BD=3\cdot\dfrac{20}{7}=\dfrac{60}{7}\left(cm\right);CD=4\cdot\dfrac{20}{7}=\dfrac{80}{7}\left(cm\right)\)
c: Ta có: \(\dfrac{BD}{CD}=\dfrac{AB}{AC}=\dfrac{3}{4}\)
=>\(S_{ABD}=\dfrac{3}{4}\cdot S_{ACD}\)
=>\(\dfrac{S_{ABD}}{S_{ACD}}=\dfrac{3}{4}\)
d: Ta có: DE\(\perp\)AC
AB\(\perp\)AC
Do đó: DE//AB
Xét ΔCAB có DE//AB
nên \(\dfrac{CD}{CB}=\dfrac{DE}{AB}\)
=>\(\dfrac{DE}{12}=\dfrac{80}{7}:20=\dfrac{4}{7}\)
=>\(DE=12\cdot\dfrac{4}{7}=\dfrac{48}{7}\left(cm\right)\)
AH
Akai Haruma
Giáo viên
13 tháng 1
Lời giải:
a. Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{12^2+16^2}=20$ (cm)
Áp dụng tính chất đường phân giác:
$\frac{BD}{DC}=\frac{AB}{AC}=\frac{12}{16}=\frac{3}{4}$
Mà: $BD+DC=BC=20$ nên:
$BD=20:(3+4).3=\frac{60}{7}$ (cm)
$CD= 20:(3+4).4=\frac{80}{7}$ (cm)
b.
$AH=2S_{ABC}:BC=\frac{AB.AC}{BC}=\frac{12.16}{20}=9,6$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{12^2-9,6^2}=7,2$ (cm)
$HD = BD-BH = \frac{60}{7}-7,2=\frac{48}{35}$ (cm)
$AD = \sqrt{AH^2+HD^2}=\sqrt{9,6^2+(\frac{48}{35})^2}=\frac{48\sqrt{2}}{7}$ (cm)
22 tháng 4 2015
a) Xét \(\Delta HAC\) và \(\Delta ABC\) có :
Góc AHC = góc BAC = 90o; góc C chung
=> \(\Delta HAC\) đồng dạng với \(\Delta ABC\) (g.g)
b) Vì \(\Delta ABC\) vuông tại A nên AB2 + AC2 = BC2 => AB2 = BC2 - AC2 = 202 - 162 = 144
=> \(AB=\sqrt{144}=12\left(cm\right)\)
Từ a) => \(\frac{AH}{AB}=\frac{AC}{BC}\) hay \(\frac{AH}{6}=\frac{8}{10}\) => \(AH=\frac{6.8}{10}=4,8\left(cm\right)\)
c) Ta có \(\Delta ABD\) đồng dạng với \(\Delta HBI\) (g.g) ('Bạn tự chứng minh')
=> Góc BIH = góc ADB
Mà góc BIH = góc AID (đ2) => Góc AID = góc ADB
=> Tam giác AID cân tại A
d) ('Mình ko biết')
28 tháng 7 2016
a) Xét \(\Delta HAC\) và \(\Delta ABC\) có :
Góc AHC = góc BAC = 90o; góc C chung
=> \(\Delta HAC\) đồng dạng với \(\Delta ABC\) (g.g)
b) Vì \(\Delta ABC\) vuông tại A nên AB2 + AC2 = BC2 => AB2 = BC2 - AC2 = 202 - 162 = 144
=> \(AB=\sqrt{144}=12\left(cm\right)\)
Từ a) => \(\frac{AH}{AB}=\frac{AC}{BC}\) hay \(\frac{AH}{6}=\frac{8}{10}\) => \(AH=\frac{6.8}{10}=4,8\left(cm\right)\)
c) Ta có \(\Delta ABD\) đồng dạng với \(\Delta HBI\) (g.g) ('Bạn tự chứng minh')
=> Góc BIH = góc ADB
Mà góc BIH = góc AID (đ2) => Góc AID = góc ADB
=> Tam giác AID cân tại A
6 tháng 4 2018
a) Xét tam giác HAB và HAC ,ta có :
Cạnh AH chung (1)
\(\widehat{BAH}=\widehat{CAH}\)( phân giác AH ) (2)
AB = AC ( gt )(3)
Từ (1)(2)(3) => tam giác HAB = HAC ( c. g. c )
b) Ta có trong tam giác cân ABC có AH là đường cao cũng là đường trung tuyến
=> G là giao của2 đường trung tuyến AH và BD
=> G là trọng tâm của tam giác ABC
p/s tham khảo
29 tháng 7 2023
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: BC=căn 12^2+16^2=20cm
c: AD là phân giác
=>BD/CD=AB/AC=3/4
=>S ABD/S ACD=3/4
d: BD/CD=3/4
=>BD/3=CD/4
mà BD+CD=10
nên BD/3=CD/4=10/7
=>BD=30/7cm; CD=40/7cm
15 tháng 3 2022
1: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó: ΔABC\(\sim\)ΔHBA
2 Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
10 tháng 5 2022
a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
góc C chung
Do đó: ΔABC\(\sim\)ΔHAC
b: Ta có: ΔABC\(\sim\)ΔHAC
nên AC/HC=BC/AC
hay \(AC^2=BC\cdot HC\)
c: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
10 tháng 5 2022
a, Xét Δ ABC và Δ HAC, có :
\(\widehat{ACB}=\widehat{HCA}\) (góc chung)
\(\widehat{BAC}=\widehat{AHC}=90^o\)
=> Δ ABC ∾ Δ HAC (g.g)
b, Ta có : Δ ABC ∾ Δ HAC (cmt)
=> \(\dfrac{AC}{HC}=\dfrac{BC}{AC}\)
=> \(AC^2=BC.HC\)
c, Xét Δ ABC, có :
\(BC^2=AB^2+AC^2\) (định lí Py - ta - go)
=> \(BC^2=3^2+4^2\)
=> \(BC^2=25\)
=> \(BC=5\left(cm\right)\)