cho f(x)+g(x)=x2+1 và g(x)-f(x)=2x.Tìm đa thức f(x) và g(x)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 8 2021
a: \(F\left(x\right)=x^5-3x^2+x^3-x^2-2x+5\)
\(=x^5+x^3-4x^2-2x+5\)
\(G\left(x\right)=x^5-x^4+x^2-3x+x^2+1\)
\(=x^5-x^4+2x^2-3x+1\)
b: Ta có: \(H\left(x\right)=F\left(x\right)+G\left(x\right)\)
\(=x^5+x^3-4x^2-2x+5+x^5-x^4+2x^2-3x+1\)
\(=2x^5-x^4+x^3-2x^2-5x+6\)
CM
3 tháng 7 2018
* Ta có:
f(x) = x5 – 3x2 + 7x4 – 9x3 + x2 - 1/4 x
= x5 – (3x2 – x2) + 7x4 – 9x3 -1/4.x
= x5 – 2x2 + 7x4 – 9x3 -1/4.x
= x5 + 7x4 – 9x3 – 2x2 - 1/4
g(x) = 5x4 – x5 + x2 – 2x3 + 3x2 - 1/4
= 5x4 –x5+ (x2 + 3x2) – 2x3 – 1/4
= 5x4 – x5 + 4x2 – 2x3 – 1/4
= -x5 + 5x4 – 2x3 + 4x2 - 1/4
* f(x) + g(x)
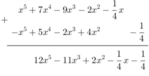
* f(x) - g(x)
22 tháng 5 2021
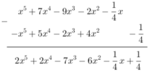
`a)f(x)+g(x)`
`=x^2+3x-5+x^2+2x+3`
`=(x^2+x^2)+(3x+2x)+(3-5)`
`=2x^2+5x-2`
`b)f(x)-g(x)`
`=x^2+3x-5-(x^2+2x+3)`
`=(x^2-x^2)+(3x-2x)-(3+5)`
`=x-8`
CM
8 tháng 9 2018
Ta có f(1) = 12 -(m - 1).1 + 3m - 2 = 2m
g(2) = 22 - 2(m + 1).2 - 5m + 1 = -9m + 1
Vì f(1) = g(2) ⇒ 2m = -9m + 1 ⇒ 11m = 1 ⇒ m = 1/11. Chọn D
30 tháng 6 2023
a: f(x)=3x^4+2x^3+6x^2-x+2
g(x)=-3x^4-2x^3-5x^2+x-6
b: H(x)=f(x)+g(x)
=3x^4+2x^3+6x^2-x+2-3x^4-2x^3-5x^2+x-6
=x^2-4
f(x)-g(x)
=3x^4+2x^3+6x^2-x+2+3x^4+2x^3+5x^2-x+6
=6x^4+4x^3+11x^2-2x+8
c: H(x)=0
=>x^2-4=0
=>x=2 hoặc x=-2
CM
18 tháng 12 2017
Ta có
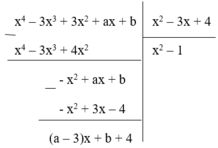
Phần dư của phép chia f(x) cho g(x) là R = (a – 3)x + b + 4. Để phép chia trên là phép chia hết thì R = 0, Ɐx
ó (a – 3)x + b + 4 = 0, Ɐx ó a - 3 = 0 b + 4 = 0
ó a = 3 b = - 4 => ab = -12
Đáp án cần chọn là: A
Cộng vế theo vế hai phương trình, ta được: f(x)+g(x)+g(x)-f(x)=x2+1+2x \(\Leftrightarrow\) 2g(x)=x2+2x+1 \(\Leftrightarrow\) g(x)=\(\dfrac{1}{2}\)x2+x+\(\dfrac{1}{2}\).
Thế g(x) vào một trong hai phương trình, ta suy ra f(x)=\(\dfrac{1}{2}\)x2-x+\(\dfrac{1}{2}\).