cho tam giác ABC có góc A:B:C=1:2:3. Tính số đo các góc trong tam giác ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Do tổng 3 góc của 1 tam giác bằng `180^o` nên:
`a, A:B:C=2:7:1`
`<=> A/2 = B/7 = C/1 = (A+B+C)/(2+7+1)=180/10=18`.
`=> A/2=18 <=> A=36^o`.
`B/7=18 <=> B=18*7=126^o`.
`C/1=18 <=> C=18^o`.
Vậy ...
`b, hat(A) + hat(C) = 180^o- hat(B)`
`<=> hat(A)+hat(C)=105^o`
Áp dụng tính chất dãy tỉ số bằng nhau:
`A/3=C/2=(A+C)/(3+2)=105/5=21.`
`=> A/3=21 <=> A=61^o`.
`=> C/2=21 <=> C=42^o`.
Vậy...
a) Gọi a, b, c lần lượt là số đo góc A, góc B và góc C
Do a : b : c = 2 : 7 : 1 nên:
a/2 = b/7 = c/1
Lại có: a + b + c = 180⁰ (tổng ba góc trong tam giác ∆ABC)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
a/2 = b/7 = c/1 = (a + b + c)/(2 + 7 + 1) = 180/10 = 18
a/2 = 18 ⇒ a = 18.2 = 36
b/7 = 18 ⇒ b = 18.7 = 126
c/1 = 18 ⇒ c = 18
Vậy số đo các góc A, góc B, góc C lần lượt là: 36⁰; 126⁰; 18⁰
b) Gọi a, c lần lượt là số đo các góc A và góc C
Do a : c = 3 : 2
⇒ a/3 = c/2
Lại có:
a + c = 180⁰ - 75⁰ = 105⁰ (tổng ba góc trong tam giác ∆ABC)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
a/3 = c/2 = (a + b)/(3 + 2) = 105/5 = 21
a/3 = 21 ⇒ a = 21.3 = 63
b/2 = 21 ⇒ b = 21.2 = 42
Vậy số đo các góc A, góc B, góc C lần lượt là: 63⁰; 75⁰; 42⁰

a) Xét ΔABC có
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)(Định lí tổng ba góc trong một tam giác)
Ta có: \(\widehat{A}:\widehat{B}:\widehat{C}=6:2:1\)
nên \(\dfrac{\widehat{A}}{6}=\dfrac{\widehat{B}}{2}=\dfrac{\widehat{C}}{1}\)
mà \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)(cmt)
nên \(\dfrac{\widehat{A}}{6}=\dfrac{\widehat{B}}{2}=\dfrac{\widehat{C}}{1}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}}{6+2+1}=\dfrac{180^0}{9}=20^0\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{\widehat{A}}{6}=20^0\\\dfrac{\widehat{B}}{2}=20^0\\\dfrac{\widehat{C}}{1}=20^0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\widehat{A}=120^0\\\widehat{B}=40^0\\\widehat{C}=20^0\end{matrix}\right.\)
Vậy: \(\widehat{A}=120^0\); \(\widehat{B}=40^0\); \(\widehat{C}=20^0\)

Bài 1:
Số đo góc ngoài tại đỉnh C là \(74^0+47^0=121^0\)
Câu 2:
Đặt \(\widehat{D}=a;\widehat{E}=b\)
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}a-b=52\\a+b=140\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=96\\b=44\end{matrix}\right.\)
Bài 3:
Theo đề, ta có: x+2x+3x=180
=>6x=180
=>x=30
=>\(\widehat{A}=30^0;\widehat{B}=60^0;\widehat{C}=90^0\)

Ta có A,B,C tỉ lệ với 1,2,3
==>A/1=B/2=C/3
==> A+B+C/1+2+3=180ĐỘ/6=30 ĐỘ nhớ tính nha

Gọi a, b, c (độ) lần lượt là số đo 3 góc A, B, C. (0 < a; b; c < 180º).
Theo định lí tổng ba góc của tam giác ta có:
a + b + c = 180.
Vì số đo 3 góc tỉ lệ với 3; 5; 7 nên ta có:
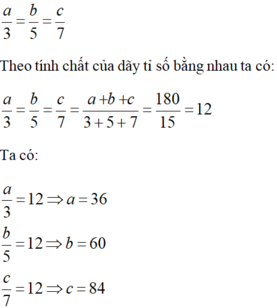
Vậy số đo ba góc của tam giác ABC là: 36o; 60o; 84o
Gọi số đo 3 góc A;B;C lần lượt là a;b;c
Áp dụng t/c của dãy tỉ số bằng nhau ta có
=>\(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}=\frac{a+b+c}{1+2+3}=\frac{180"}{6}=30"\)
=>a=30"
b=60"
c=90"
Vậy....................
Chuk bn hok tốt
ta có:
A:B:C=1:2:3
\(\Rightarrow\frac{A}{1}=\frac{B}{2}=\frac{C}{3}\)và \(A+B+C=180\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{A}{1}=\frac{B}{2}=\frac{C}{3}=\frac{A+B+C}{1+2+3}=30\)
\(\Rightarrow\frac{A}{1}=30\Rightarrow A=30\)
\(\frac{B}{2}=30\Rightarrow B=60\)
\(\frac{C}{3}=30\Rightarrow C=90\)
Vậy A=30 độ ; B=60 độ : C=90 độ