Câu 2: Giải các hệ phương trình sau:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) 3 x 2 – 7x + 2 = 0
Δ= 7 2 -4.3.2 = 49 - 24 = 25 > 0 ⇒ ∆ = 5
Phương trình có 2 nghiệm phân biệt:
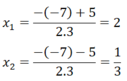
Vậy tập nghiệm của phương trình là S = {2; 1/3}


Thay x = 3, y = 5 vào vế trái của phương trình (3) ta được:
VT = 5.3 – 2.5 = 15 – 10 = 5 = VP
Vậy (x; y) = (3; 5) là nghiệm của phương trình (3).
Hệ phương trình đã cho có nghiệm (x; ) = (3; 5)


Thay x = -3, y = 31/5 vào vế trái của phương trình (2), ta được:
VT = -3.(-3) + 2.31/5 = 9 + 62/5 = 107/5 ≠ 22 = VP
Vậy (x; y) = (-3; 31/5 ) không phải là nghiệm của phương trình (2).
Hệ phương trình đã cho vô nghiệm.

( 2 m - 1 ) 2 - 4 ( m + 1 ) ( m - 2 ) ≥ 0 ⇔ 9 ≥ 0. Bất phương trình có tập nghiệm là R.

7 x - 3 y = 5 1 4 x + y = 2 2
Từ (2) rút ra được y = -4x + 2.
Thế y = -4x + 2 vào phương trình (1) ta được :
7x – 3.(-4x+2) = 5 ⇔ 7x + 12x – 6 = 5 ⇔ 19x = 11 ⇔ 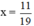
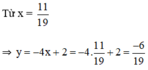
Vậy hệ phương trình có nghiệm duy nhất 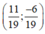

x - y = 3 3 x - 4 y = 2
Từ (1) rút ra được y = x – 3
Thế vào phương trình (2) ta được:
3x – 4.(x – 3) = 2 ⇔ 3x – 4x + 12 = 2 ⇔ x = 10
Từ x = 10 ⇒ y = x – 3 = 7.
Vậy hệ phương trình có nghiệm duy nhất (10 ; 7).
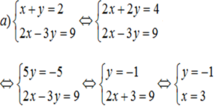
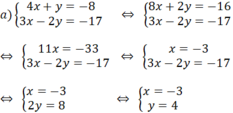

\(a,\left\{{}\begin{matrix}x+2y=5\\3x+4y=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=5-2y\\3\left(5-2y\right)+4y=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=5-2y\\15-6y+4y=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=5-2y\\15-2y=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=5-2.5\\y=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=-5\\y=5\end{matrix}\right.\)
\(b,\left\{{}\begin{matrix}3x+y=3\\2x-y=7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3-3x\\2y-\left(3-3x\right)=7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3-3x\\2y-3+3x=7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3-3x\\5x-3=7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3-3.2\\x=2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-3\\x=2\end{matrix}\right.\)
mik c.ơn