Tính thể tích của hình chóp tam giác đều, biết cạnh bên bằng 5cm và chiều cao bằng 4cm.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
17 tháng 5 2019
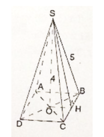
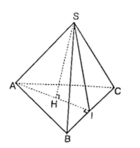
a) Ta có
OC2 = SC2 - SO2 (Pytago)
= 52 - 42 = 9(cm)
=> OC = 3(cm)
=> AC = 6(cm)
AB2 + BC2 = AC2 (pytago)
2BC2 = AC2 (do AB = BC)
BC2 = AC2/2 = 36/2 = 18(cm)
BC = √18 = 3√2 (cm)
Gọi K là trung điểm của BC. Tam giác SBC cân tại S có SH là đường trung tuyến nên SH cũng là đường cao. Suy ra SH ⊥ BC
Do đó
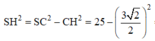
![]()

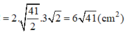
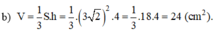

CM
19 tháng 1 2017
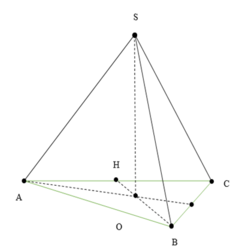
Chọn C
Phương pháp:

Cách giải:
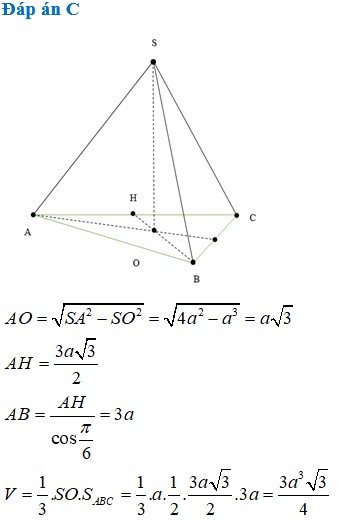
Hình chóp tam giác đều ABC có chiều cao a, cạnh bên 2a.
Gọi H là trọng tâm tam giác ABC => SH là đường cao hình chóp => SH = a
Gọi I là trung điểm BC
Do tam giác ABC đều

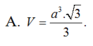
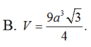
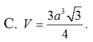
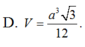
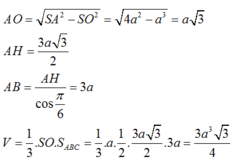

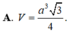
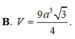

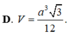


Sorry cho sửa lại
Thể tích hình chóp là: \(V=\dfrac{1}{3}\cdot4\cdot\dfrac{27\sqrt{3}}{4}=9\sqrt{3cm^3}\)
hình chóp tam giác đều có độ dài cạnh bên là 5cm, chiều cao là 4cm.
⇒nửa đường chéo của hình vuông đấy là 3cm
⇒đường chéo của đáy là 6cm.
diện tích đáy là:\(\frac{1}{2} × 6×6=18\)(cm²)
Thể tích hình chóp là:
\(ADC:V=\frac{1}{3} S.H=\frac{1}{3}×18×4=24\)(cm³)
Vậy…