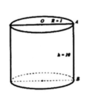
Một chiếc ống bằng gỗ có dạng hình trụ rỗng chiều cao h = 10cm, bán kính trong R1 = 8cm, bán kính ngoài R2 = 10cm. Khối lượng riêng của gỗ làm ống là D1 = 800kg/m3, ống không thấm nước và xăng. a) Ban đầu người ta dán kín một đầu bằng nilon mỏng (đầu này được gọi là đáy). Đổ đầy xăng vào ống rồi nhẹ nhàng đẩy ống xuống nước theo phương thẳng đứng sao cho xăng không tràn ra ngoài. Tìm chiều cao phần nổi của ống biết khối lượng riêng của xăng là D2 = 750kg/m3, của nước là D0 = 1000kg/m3. b) Đổ hết xăng ra khỏi ống, bóc đáy nilon đi và đặt ống trở lại trong nước theo phương thẳng đứng, sau đó từ từ đổ xăng vào ống. Tìm khối lượng xăng tối đa có thể đổ vào trong ống.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tui đang thấy đề bài lạ lắm đây, cho bán kính trong mà ko cho bán kính ngoài, vậy thì không lẽ ống gỗ này có rìa mỏng? Nếu vậy thì trọng lượng của ống sẽ ko đáng kể, mà muốn tìm được Dống thì phải áp dụng ct Pống= Dống.Sống.10, trọng lượng ko đáng kể thì tìm kiểu gì nhỉ?
Tui trình bày cách làm của tui ra đây, nếu tui ko nhầm thì bài này cho thiếu bán kính ngoài
\(V_{xang}=\dfrac{m}{D_{xang}}=...\left(m^3\right)\)
\(V_{xang}=S_{trong}.l_{xang}=\pi R^2_{trong}.l_{xang}\left(m^3\right)\)
\(\Rightarrow\pi R^2_{trong}.l_{xang}=\dfrac{m}{D_{xang}}\Rightarrow l_{xang}=...\left(m\right)\)
Chọn một điểm nằm ở mặt phân cách giữa xăng và nước
\(\Rightarrow p_{xang}=p_{nuoc}\Leftrightarrow d_{xang}.l_{xang}=d_{nuoc}.h_{chim}\)
\(\Rightarrow h_{chim}=\dfrac{d_{xang}.l_{xang}}{d_{nuoc}}=...\left(m\right)\)
\(P_{ong}+P_{xang}=F_A\Leftrightarrow10.D_{ong}.l\left(R_{ngoai}^2-R_{trong}^2\right)+10.D_{xang}.l_{xang}.\pi R_{trong}^2=10.D_{nuoc}.h_{chim}.\pi R_{ngoai}^2\)
\(\Rightarrow D_{ong}=...\left(kg/m^3\right)\)