Giúp e trình bày chi tiết đi ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 3 2022
\(\left\{{}\begin{matrix}u_3=13\\u_5=23\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_1+2d=13\\u_1+4d=23\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}u_1=3\\d=5\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 3 2022
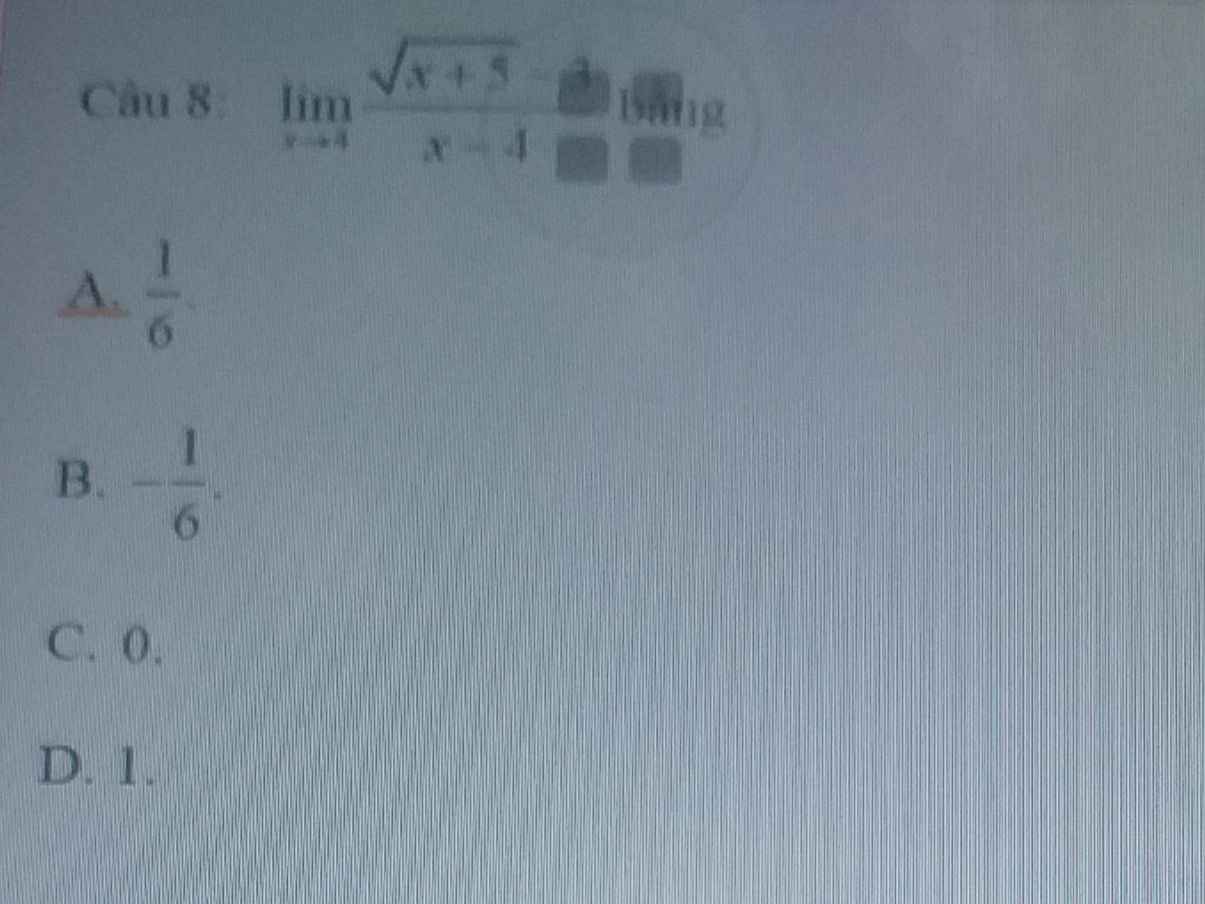
\(\lim\limits_{x\rightarrow4}\dfrac{\sqrt{x+5}-3}{x-4}=\lim\limits_{x\rightarrow4}\dfrac{\left(\sqrt{x+5}-3\right)\left(\sqrt{x+5}+3\right)}{\left(x-4\right)\left(\sqrt{x+5}+3\right)}\)
\(=\lim\limits_{x\rightarrow4}\dfrac{x-4}{\left(x-4\right)\left(\sqrt{x+5}+3\right)}=\lim\limits_{x\rightarrow4}\dfrac{1}{\sqrt{x+5}+3}=\dfrac{1}{3+3}=\dfrac{1}{6}\)
KB
4 tháng 5 2022
\(y=\dfrac{x-1}{x+2}\left(x\ne-2\right)\Rightarrow y'=\dfrac{\left(x+2\right)-\left(x-1\right)}{\left(x+2\right)^2}=\dfrac{3}{\left(x+2\right)^2}\)
Giả sử d là tiếp tuyến cần tìm của đths trên
a. d đi qua \(N\left(-1;-2\right)\) . Suy ra : HSG của d : \(\dfrac{3}{\left(-1+2\right)^2}=3\)
PTTT d : \(y=3\left(x+1\right)-2=3x+1\)
b.d có hđtđ \(x_o=3\) \(\Rightarrow y_o=\dfrac{3-1}{3+2}=\dfrac{2}{5};y'=\dfrac{3}{25}\)
PTTT d : \(y=\dfrac{3}{25}\left(x-3\right)+\dfrac{2}{5}=\dfrac{3x}{25}+\dfrac{1}{25}\)
c. Tung độ tiếp điểm yo = 9 nên : \(\dfrac{x_o-1}{x_o+2}=9\Leftrightarrow x_o=-\dfrac{19}{8}\)
y' = 64/3
PTTT d : \(y=\dfrac{64}{3}\left(x+\dfrac{19}{8}\right)+9=\dfrac{64}{3}x+\dfrac{179}{3}\)
d. Ta có : \(\dfrac{3}{\left(x_o+2\right)^2}=\dfrac{1}{3}\Leftrightarrow\left[{}\begin{matrix}x_o+2=3\\x_o+2=-3\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x_o=1\\x_o=-5\end{matrix}\right.\)
Với xo = 1 \(\Rightarrow y_o=0\) . PTTT d : y = 1/3(x-1) = 1/3x - 1/3
Với xo = -5 \(\Rightarrow y_o=2\) . PTTT d : \(y=\dfrac{1}{3}\left(x+5\right)+2=\dfrac{1}{3}x+\dfrac{11}{3}\)
NH
1
31 tháng 8 2021
Bài 1:
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HF là đường cao ứng với cạnh huyền AB, ta được:
\(AF\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)
10 tháng 12 2021
Bài 6:
Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
Hàm \(f\left(x\right)\) ko xác định khi \(x+4=0\Rightarrow x=-4\)
\(\Rightarrow\) Hàm gián đoạn tại \(x=-4\)