Tính SABC, biết BC=2cm, Â=1050, góc C=300
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.
Trong tam giác vuông ABH ta có:
\(cotB=\dfrac{BH}{AH}\Rightarrow BH=AH.cotB\)
Trong tam giác vuông ACH ta có:
\(cotC=\dfrac{CH}{AH}\Rightarrow CH=AH.cotC\)
\(\Rightarrow BH+CH=AH.cotB+AH.cotC\)
\(\Leftrightarrow BC=AH\left(cotB+cotC\right)\)
\(\Leftrightarrow AH=\dfrac{BC}{cotB+cotC}\) (đpcm)
b. Áp dụng công thức câu a:
\(AH=\dfrac{4}{cot45^0+cot30^0}=-2+2\sqrt{3}\) (cm)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.\left(-2+2\sqrt{3}\right).4=-4+4\sqrt{3}\approx2,93\left(cm^2\right)\)


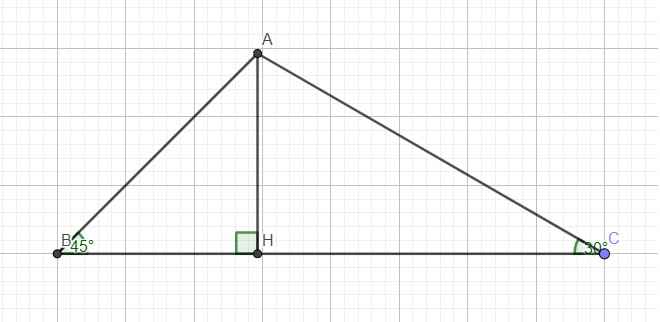
A B C H x x
kẻ đường cao AH đặt AH=x
tam giác AHB có góc AHB=90 độ=>góc HAB=góc HBA=45 độ
=>tam giác AHB vuông cân tại H=>BH=AH=x
tam giác AHC vuông tại H=> \(AC^2=AH^2+HC^2=x^2+\left[2-x\right]^2\)[1]
tam giác AHC có góc H=90độ góc C=30 độ => góc HAC=60 độ=> \(HC=\frac{AC.\sqrt{3}}{2}suyraAC=\frac{2HC}{\sqrt{3}}suyraAC^2=\frac{4HC^2}{3}\)[2]
[1,2]=>\(x^2+\left[2-x\right]^2=\frac{4\left[2-x\right]^2}{3}\)
giải phương trình =>x=\(\sqrt{3}-1\)
Sabc=1/2.BC.AH=\(\frac{1}{2}.2.\left[\sqrt{3}-1\right]=\sqrt{3}-1cm^2\)


Chọn đáp án A
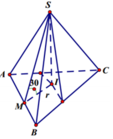
+ Dễ thấy tam giác ABC vuông tại B.
![]()
+ Gọi p là nửa chu vi
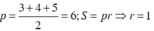
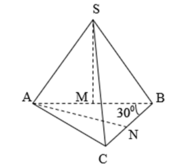
+ Gọi I là tâm đường tròn nội tiếp tam giác từ giả thiết các mặt bên tạo với đáy ABC một góc 30 độ ta suy ra I là chân đường cao của khối chóp
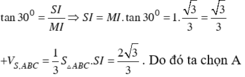

\(\text{Xét}:\)\(\Delta CDE\)\(\text{và}\)\(\Delta CAB\)\(,\)\(\text{ta có:}\)
\(\widehat{C}\)\(:\)\(chung\)
\(\widehat{CDE}=\widehat{CAB}=90^o\)
\(\Rightarrow\Delta CDE\text{∽}\Delta CAB\left(g-g\right)\)
\(\Rightarrow\frac{CD}{DE}=\frac{CA}{AB}\)\(\text{hay}\)\(\frac{2}{DE}=\frac{4}{6}\)
\(\Rightarrow DE=\left(6.2\right):4=3\left(cm\right)\)
tích rồi mình mới trả lời