Có 7 đoạn thẳng: a1;a2;a3;a4;a5;a6;a7 có độ dài lớn hơn 10 và nhỏ hơn 100 thỏa mãn 10<a1<a2<a3<a4<a5<a6<a7<100. CMR: tồn tại một cặp gồm 3 đoanh thẳng có thể tạo thành 1 tam giác
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, cứ 1 điểm ta nối đc với 4 điểm còn lại tạo thành: 4 đường thẳng
có 5 điểm như vậy nên vẽ được: 4.5=20 (đường thẳng )
nhưng nếu tính như vậy mỗi đường thẳng sẽ được tính 2 lần nên vẽ được:
20:2=10 (đường thẳng)
Đáp số: 10 đường thẳng

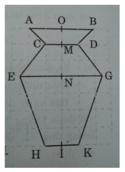
a) - Trung điểm của đoạn AB là điểm O.
- M là trung điểm của đoạn CD.
- N là trung điểm của đoạn EG.
- I là trung điểm của đoạn thẳng HK.
b) Trong các đoạn thẳng AB, CD, EG và HK:
- Đoạn thẳng có độ dài lớn nhất là EG.
- Hai đoạn thẳng có độ dài bằng nhau là CD và KH.

1> có số đoạn thẳng là
5.(5-1)/2=10
những đoạn thẳng đó là
AB,AC,AD,AE,BC,BD,BE,CD,CE,DE
2> có vì
trong 5 điểm k có 3 điểm nào thẳng hàng
do đó cũng k có bất kì 2 đoạn thẳng nào trùng nhau
A B C D E c

a) Chọn 1 điểm, qua điểm đó và n điểm ta được (n - 1) đoạn thẳng. Làm như vậy với n điểm ta được : n(n - 1) đoạn thẳng.
Mà mỗi đoạn thẳng được tính 2 lần nên ta được :
\(\frac{n\left(n-1\right)}{2}\) (đoạn thẳng)
b) (Hình sai đề, lặp lại đề a, mình sẽ bỏ chữ "ko" đi)
+ Với 3 điểm không thẳng hàng ta vẽ được : 3(3 - 1) : 2 = 3 (đoạn thẳng)
+ Với 3 điểm thẳng hàng ta vẽ được 3 đoạn thẳng.
Vậy số đoạn thẳng có giảm đi : 3 - 3 = 0 (đoạn thẳng)
Số đoạn thẳng không thay đổi, ta có số đoạn thẳng là :
\(\frac{n\left(n-1\right)}{2}\)
c) \(\frac{n\left(n-1\right)}{2}=1770\Rightarrow n\left(n-1\right)=1770.2\)
\(\Rightarrow n\left(n-1\right)=2^2.3.5.50=\left(2^2.3.5\right).59=60.59\)
\(\Rightarrow\) n = 60 (điểm).
Bạn có nói là học thầy Phong đúng không? Hehe, mai đi học mình "méc" thầy cho! Đề cương nghỉ Tết cũng nhờ!


số phần được chia :3+5=8 (phần)
Đoạn thẳng AO dài :64/8x3=24(dm)
Ta có : \(10< a_1< a_2< a_3< a_4< a_5< a_6< a_7< 100\)
Nếu bất kì ba đoạn thẳng nào cũng không thể lập thành một tam giác thì :
\(a_3\ge a_1+a_2\ge10+10=20\)
\(a_4\ge a_2+a_3\ge10+20=30\)
\(a_5\ge a_3+a_4\ge20+30=50\)
\(a_6\ge a_4+a_5\ge30+50=80\)
\(a_7\ge a_5+a_6\ge50+80=130\)(vô lí)
Vậy tồn tại một cặp gồm 3 đoạn thẳng có thể tạo thành một tam giác.