Một ôtô khối lượng 1,5 tấn đang chuyển động trên đưởng nằm ngang với vận tốc 10 m/s người ta đột ngột hãm phanh ô tô chuyển động thêm 20m nữa thì dừng hẳn Tính độ lớn của Lực hãm phanh.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
10 tháng 4 2022
m=4 tấn = 4000 (kg)
\(v_0=98km/h=27m/s\)
v = 0 (m/s)
s = 45m
\(a=\dfrac{v^2-v_0^2}{2.45}=\dfrac{0^2-27^2}{90}=-8,1m/s\)
Định luật II Niu-tơn:
\(\overrightarrow{F_{ms}}+\overrightarrow{N}+\overrightarrow{P}=m.\overrightarrow{a}\)
Lực hãm phanh:
\(-F_{ms}=m.a\)
\(\Rightarrow F_{ms}=-m.a=-4000.-8,1=32400\left(N\right)\)
DQ
6 tháng 1 2021
Đổi 2 tấn = 2000 kg
36 km/h = 10 m/s
a. Gia tốc của xe là:
\(a=\dfrac{\Delta v}{t}=\dfrac{0-10}{2}=-5\) (m/s)
Độ lớn của lực hãm là:
\(\left|F\right|=\left|ma\right|=10000\) (N)
Hệ số ma sát giữa xe với mặt đường là:
\(\mu=\dfrac{F}{N}=\dfrac{10000}{20000}=0,5\)
b. Quãng đường xe đi được cho đến khi dừng lại là:
\(s=\dfrac{v^2}{2a}=\dfrac{10^2}{2.5}=10\) (m)
MT
28 tháng 12 2020
m= 1,2 tấn = 1200kgv= 36km/h = 10m/st=2s
Gia tốc của xe là :a=\(\dfrac{v-v_0}{t}=\dfrac{0-10}{2}=\) -5 m/s
1) quãng đường ô tô đi được kể từ lúc giảm phanh là:
\(s=v_0t+\dfrac{1}{2}at^2\)
\(=10\cdot2+\dfrac{1}{2}\left(-5\right)\cdot2^2\) \(=10m\)
2) vì lực hãm phanh và lực ma sát giữa xe với mặt đường có giá trị bằng nhau nên
Fms = Fh
Fms = ma = 1200 * (-5) = -6000 N⇒ điều này chứng tỏ Fms ngược chừng chiều động của ô tô
N
30 tháng 11 2021
a. Ta có: \(\left\{{}\begin{matrix}s=v_0t+\dfrac{1}{2}at^2\Leftrightarrow24=v_0\cdot4+\dfrac{1}{2}\cdot a\cdot4^2\Leftrightarrow24=v_0\cdot4+8a_{\left(1\right)}\\v_0+at=0\Leftrightarrow v_0=-a\cdot4_{\left(2\right)}\end{matrix}\right.\)
Thay (2) vào (1): \(24=8a-16a\)
\(\Rightarrow a=-3\left(\dfrac{m}{s^2}\right)\)
\(\Rightarrow v_0=-at=-3\cdot-4=12\left(\dfrac{m}{s}\right)\)
b. \(F_{ham}=ma=2000\cdot-3=-6000\left(N\right)\)
c. \(F'_{ham}=3F_{ham}=3\cdot-6000=-18000\left(N\right)\)
\(F'_{ham}=ma'\Rightarrow a'=\dfrac{F'_{ham}}{m}=\dfrac{-18000}{2000}=-9\left(\dfrac{m}{s^2}\right)\)
\(v^2-v_0^2=2a'S'\)
\(\Leftrightarrow0^2-12^2=2\cdot-9\cdot S'\)
\(\Leftrightarrow-144=-18\cdot S'\)
\(\Rightarrow S'=8\left(m\right)\)
N
22 tháng 11 2021
\(2\left(tan\right)=2000kg=2\cdot10^3\) - \(60\left(\dfrac{km}{h}\right)=\dfrac{50}{3}\left(\dfrac{m}{s}\right)\)
\(v^2-v_0^2=2aS\Leftrightarrow0^2-\left(\dfrac{50}{3}\right)^2=2\cdot a\cdot50\)
\(\Rightarrow a=-\dfrac{25}{9}\left(\dfrac{m}{s^2}\right)\)
\(F_{ham}=-ma=-2\cdot10^3\cdot\left(-\dfrac{25}{9}\right)\approx5555,6\left(N\right)\)
\(v=v_0+at\Leftrightarrow0=\dfrac{50}{3}+\left(-\dfrac{25}{9}\right)\cdot t\)
\(\Rightarrow6\left(s\right)\)
VT
23 tháng 11 2017
Chọn đáp án A
? Lời giải:
+ v 2 − v 0 2 = 2as, với: v0 = 79,2 km/giờ = 22 m/s, v = 0, s = 100 m
VT
20 tháng 3 2017
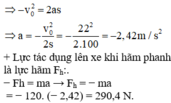
Ta có khi tàu dừng lại
v 2 = 0 ( m / s ) ; v 1 = 54 ( k m / s ) = 15 ( m / s )
Độ biến thiên động lượng
Δ p = p 2 − p 1 = − m v 1 = − 10.000.15 = − 150000 ( N )
Lực hãm để tàu dừng lại sau sau 10 giây
Δ p = F . Δ t ⇒ F = − − 150000 10 = − 15000 ( N )