Giá trị của x thuộc tập nào sau đây để thỏa mãn: \(\left|2x-4\right|=2x-4\)
A. \([2;+\infty)\)
B. \(\left(-\infty;2\right)\)
C. \((-\infty;2]\)
D. \(\left(2;+\infty\right)\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left|A\right|=A\Leftrightarrow A\ge0\)
Do đó: phương trình tương đương: \(2x-4\ge0\Leftrightarrow x\ge2\)

\(\left|x^2-4x+3\right|=x^2-4x+3\Leftrightarrow x^2-4x+3\ge0\)
\(\Rightarrow x\in(-\infty;1]\cup[3;+\infty)\)

Đáp án A
Ta có, giả thiết
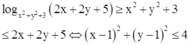
là miền trong đường tròn tâm I(1;1) bán kính R1 = 2
Và


Câu 1: Giá trị của x thỏa mãn
|x+2,37|+|y−5,3|=0
Để GTBT bằng 0 thì |x+2,37| = 0 và |y−5,3| = 0
-> x = -2,37 , y = 5,3
Vậy x = -2,37
Câu 2: Giá trị của y thỏa mãn
−|2x+\(\frac{4}{7}\)|−|y−1,37| = 0
-> |2x+\(\frac{4}{7}\) = 0 -> x = \(-\frac{2}{7}\)
-> |y−1,37| = 0 -> y = 1,37
Vậy y = 1,37

3/ bạn lập bảng xét dấu là sẽ thấy có 4 trường hợp:
TH1: x<(-5/6), khi đó: -(2x+1)+[-(3-4x)]+[-(6x+5)]=2014
-2x-1-3+4x-6x-5=2014
-4x-9=2014
x=-2023/4 ( TM x<-5/6)
TH2: -5/6<=x<=-1/2, khi đó: 2x+1+[-(3-4x)]+[-(6x+5)]=2014
2x+1-3+4x-6x-5=2014
0x-7=2014 ( ko có giá trị x TM pt)
TH3:-1/2<=x<=3/4, khi đó: 2x+1+(3-4x)+[-(6x+5)]=2014
2x+1+3-4x-6x-5=2014
-8x-1=2014
x=-2015/8 ( ko TM -1/2<=x<=3/4 )
TH4: x>3/4; khi đó: 2x+1+3-4x+6x+5=2014
4x+9=2014
x=2005/4( TM x>3/4)
thế là xong. cái nào TM thì lấy
ghi chú <= là nhỏ hơn hoặc bằng
ĐK: \(x\ge2\)
PT \(\Leftrightarrow\left[{}\begin{matrix}2x-4=2x-4\\2x-4=4-2x\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x\in R\\x=2\end{matrix}\right.\)
Kết hợp với điều kiện \(\Rightarrow x\ge2\)
Vậy \(x\in[2;+\infty)\)