gải giúp mk bài 3,4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 10 2021
Bài 3:
a: \(M=5+5^2+5^3+...+5^{99}+5^{100}\)
\(=5\left(1+5\right)+...+5^{99}\left(1+5\right)\)
\(=6\cdot\left(5+...+5^{99}\right)⋮6\)
b: \(N=1+4+4^2+...+4^{62}\)
\(=\left(1+4+4^2\right)+...+4^{60}\left(1+4+4^2\right)\)
\(=21\cdot\left(1+...+4^{60}\right)⋮21\)
J
1
19 tháng 9 2016
+) Cách nói châm biếm, phép điệp từ, hình ảnh đối lập, bài ca dao là lời chế giễu những hạng người nghiện ngập, lười biếng, thích đc hưởng thụ. 
+) Cách nói nhại lại lời thầy bói, kết cấu "chẳng-thì", tạo ra cách nói nước đôi. Bài ca dao 4 châm biếm những kẻ hành nghề mê tín, lừa đảo bịp bợm để kiếm tiền, đồng thời cũng phê phán những người thiếu hiểu biết. 
Học tốt nhé
LS
1
4 tháng 12 2016
Ta có: \(\left|x-3,4\right|+\left|2,6-x\right|=0\)
\(\Rightarrow\left|x-3,4\right|=0\) và \(\left|2,6-x\right|=0\)
+) \(x-3,4=0\Rightarrow x=3,4\)
+) \(2,6-x=0\Rightarrow x=2,6\)
Nhưng \(x\ne x\Rightarrow\) vô lí
Vậy không có giá trị x thỏa mãn đề bài
8 tháng 9 2021
\(1,\\ a,x^2\left(x-2x^3\right)=x^3-2x^5\\b,\left(x^2+1\right)\left(5-x\right)=5x^2-x^3+5-x\\ c,\left(x-2\right)\left(x^2-3x+4\right)=x^3-2x^2-3x^2+6x+4x-8=x^3-5x^2+10x-8\\ d,\left(x-2\right)\left(x-x^2+4\right)=x^2-x^3+4x-2x+2x^2-8=3x^2-x^3+2x-8\\ e,\left(x^2-1\right)\left(x^2+2x\right)=x^4-2x^3-x^2-2x\\ f,\left(x-1\right)\left(x+1\right)=x^2-1 \)
8 tháng 9 2021
\(3,\\ a,1-2y+y^2=\left(y-1\right)^2\\ b,\left(x+1\right)^2-25=\left(x+6\right)\left(x-4\right)\\ c,1-4x^2=\left(1-2x\right)\left(1+2x\right)\\ d,8-27x^3=\left(2-3x\right)\left(4+6x+9x^2\right)\\ e,27+27x+9x^2+x^3=\left(x+3\right)^3\\ f,8x^3-12x^2y+6xy^2-y^3=\left(2x-y\right)^3\\ g,x^3+8y^3=\left(x+2y\right)\left(x^2-2xy+4y^2\right)\)
3 tháng 3 2022
Bài 1:
a)\(\dfrac{15}{8}-\dfrac{11}{8}=\dfrac{4}{8}\)
b) \(\dfrac{22}{9}-\dfrac{7}{9}=\dfrac{15}{9}\)
c)\(\dfrac{7}{6}-\dfrac{4}{5}=\dfrac{35}{30}-\dfrac{24}{30}=\dfrac{11}{30}\)
d) \(\dfrac{11}{12}-\dfrac{2}{3}=\dfrac{11}{12}-\dfrac{8}{12}=\dfrac{3}{12}=\dfrac{1}{4}\)
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 1 2024
a.
Do C là giao điểm 2 tiếp tuyến tại A và M
\(\Rightarrow AC=MC\)
Tương tự có \(BD=MD\)
\(\Rightarrow AC+BD=MC+MD=CD\)
2.
Cũng theo t/c hai tiếp tuyến cắt nhau ta có:
\(\left\{{}\begin{matrix}\widehat{COA}=\widehat{COM}\\\widehat{DOB}=\widehat{DOM}\end{matrix}\right.\)
\(\Rightarrow\widehat{COA}+\widehat{COM}+\widehat{DOB}+\widehat{DOM}=2\left(\widehat{COM}+\widehat{DOM}\right)\)
\(\Rightarrow180^0=2\widehat{COD}\)
\(\Rightarrow\widehat{COD}=90^0\)
Hay tam giác COD vuông tại O
Trong tam giác vuông COD, do CD là tiếp tuyến tại M \(\Rightarrow OM\perp CD\)
\(\Rightarrow OM\) là đường cao ứng với cạnh huyền
Áp dụng hệ thức lượng:
\(OM^2=CM.MD\Rightarrow R^2=AC.BD\) (do \(AC=CM;BD=MD\))
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 1 2024
3.1
Theo cmt ta có \(AC=MC\)
Lại có \(OA=OM=R\)
\(\Rightarrow OC\) là trung trực của AM
\(\Rightarrow OC\perp AM\) tại E
\(\Rightarrow\widehat{OEM}=90^0\)
Hoàn toàn tương tự ta có \(\widehat{OFM}=90^0\)
\(\Rightarrow OEMF\) là hình chữ nhật (tứ giác vó 3 góc vuông)
3.2
\(OM\perp CD\Rightarrow\Delta OCM\) vuông tại M
\(ME\perp OC\Rightarrow ME\) là đường cao trong tam giác vuông OCM
Áp dụng hệ thức lượng:
\(OM^2=OE.OC\Rightarrow OE.OC=R^2\)
Hoàn toàn tương tự ta có: \(OM^2=OF.OD\)
\(\Rightarrow OE.OC=OF.OD=R^2\)
3.3
Do OC là trung trực AM (chứng minh câu 3.1) \(\Rightarrow E\) là trung điểm AM
Tương tự ta có F là trung điểm BM
\(\Rightarrow EF\) là đường trung bình tam giác MAB
\(\Rightarrow EF||AB\)
Mà \(AB\perp BD\) (do BD là tiếp tuyến tại B)
\(\Rightarrow EF\perp BD\)
3.4
Gọi G là trung điểm CD.
Do tam giác COD vuông tại O (theo cm câu 2) \(\Rightarrow\) G là tam đường tròn ngoại tiếp tam giác COD
Hay \(GO\) là 1 bán kính của đường tròn đường kính CD (1)
\(CA\) và BD cùng vuông góc AB \(\Rightarrow CA||BD\Rightarrow ACDB\) là hình thang
O là trung điểm AB, G là trung điểm CD \(\Rightarrow OG\) là đường trung bình hình thang ACDB
\(\Rightarrow GO||DB\Rightarrow GO\perp AB\) tại G (2)
(1);(2)\(\Rightarrow AB\) là tiếp tuyến của đường tròn đường kính CD
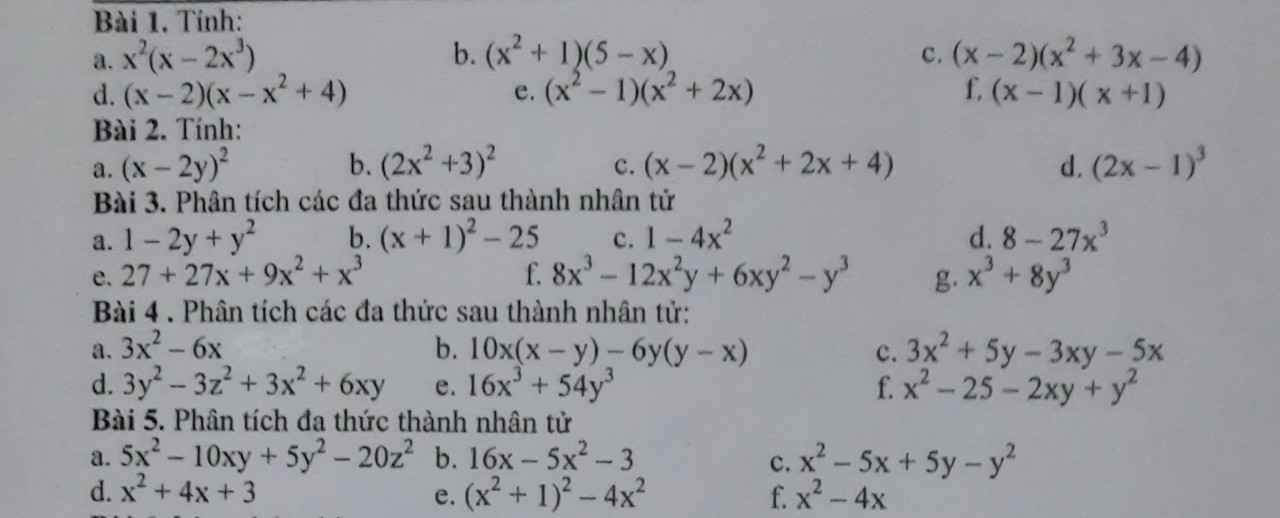
B A C H 9 25 K
a, Xét tam giác HBA và tam giác ABC ta có
^A = ^BHA = 900
^B _ chung
Vậy tam giác HBA ~ tam giác ABC ( g.g )
\(\Rightarrow\frac{HB}{AB}=\frac{AB}{BC}\)( tỉ số đồng dạng )
\(\Rightarrow AB^2=HB.BC\)
\(\Rightarrow AB^2=9.25=225\Rightarrow AB=15\)cm
b, Áp dụng đinh lí Py ta go cho tam giác ABC vuông tại A
\(BC^2=AB^2+AC^2\Rightarrow AC^2=BC^2-AB^2\)
\(\Rightarrow AC^2=625-225=400\Rightarrow AC=20\)cm
Aps dụng định lí Py ta go cho tam giác BHA vuông tại H ta có :
\(AB^2=BH^2+HA^2\Rightarrow HA^2=AB^2-BH^2=225-81\)
\(\Rightarrow AH^2=144\Rightarrow AH=12\)cm
Vì AK là tia phân giác nên : \(\frac{AH}{AC}=\frac{HK}{KC}\Rightarrow\frac{12}{20}=\frac{HK}{KC}\)
mà \(HK=HC-KC=16-KC\)(1) ( \(HC=BC-HB=25-9=16\))
hay \(\frac{12}{20}=\frac{16-KC}{KC}\Rightarrow12KC=320-20KC\)
\(\Leftrightarrow32KC=320\Leftrightarrow KC=10\)cm
Từ (1) ta lại có : \(HK=16-KC=16-10=6\)cm