Hai người cùng hoàn thành một công việc trong 12 giờ. người thứ nhất làm trong 4 giờ, người thứ hai làm trong 6 giờ thì mới được \(\dfrac{2}{5}\) công việc. Hỏi nếu làm độc lập thì mỗi người hoàn thành công việc trong bao lâu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 3 2022
Cả 2 người thợ làm cùng nhau mỗi giờ làm được
\(\dfrac{1}{4}+\dfrac{1}{6}=\dfrac{5}{12}\)( Công việc )
Cả 2 người thợ làm chung thì hoàn thành công việc sau
\(1:\dfrac{5}{12}=\dfrac{12}{5}=24h\)
7 tháng 3 2022
Gọi thời gian người thứ nhất và người thứ hai hoàn thành công việc khi làm một mình lần lượt là x,y
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\\\dfrac{4}{x}+\dfrac{6}{y}=\dfrac{5}{12}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{24}\\\dfrac{1}{y}=\dfrac{1}{24}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=24\\y=24\end{matrix}\right.\)
B
25 tháng 1 2021
Gọi 1h công nhân thứ 1,2 làm được a,ba,b (phần công việc )
Theo bài ta có :18(a+b)=1
6a+12b=1\2
{a=1\36
b=1\36
→→ Nếu làm riêng thì mỗi người hoàn thành công việc đó trong 36h
*tk
25 tháng 1 2021
Gọi thời gian người thứ nhất làm 1 mình xong công việc là x(h)
Gọi thời gian người thứ hai làm một mình xong việc là y(h),(x,y>18)
Trong 1 giờ người thứ nhất làm được :x (công việc); người thứ 2 làm được :y (công việc).
Vì 2 người cùng làm thì trong 18h thì xong việc nên nên ta có phương trình sau: x+y=118(1)
Nếu người thứ nhất làm 6h và người thứ 2 làm 12h thì chỉ hoàn thành được 50% công việc nên ta có phương trình sau: 6x+12y=50%=12(2)
Từ (1) và (2) ta có hệ phương trình:
x+y=118 và6x+12y=12
x=36(tm) và y=36(tm
Vậy thời gian người thứ nhất làm 1 mình xong công việc là 36h, thời gian người thứ hai làm một mình xong việc là 36h.
22 tháng 2 2022
Gọi thời gian làm riêng của người thứ nhất và thứ hai lần lượt là x,y
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\\\dfrac{5}{x}+\dfrac{6}{y}=\dfrac{2}{15}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{x}+\dfrac{5}{y}=\dfrac{5}{4}\\\dfrac{5}{x}+\dfrac{6}{y}=\dfrac{2}{15}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-1}{y}=\dfrac{67}{60}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\end{matrix}\right.\)
=>Đề sai rồi bạn
1 tháng 2 2021
Gọi x(giờ) và y(giờ) lần lượt là thời gian người thứ nhất và người thứ hai hoàn thành công việc khi làm một mình(Điều kiện: x>16; y>16)
Trong 1 giờ, người thứ nhất làm được: \(\dfrac{1}{x}\)(công việc)
Trong 1 giờ, người thứ hai làm được: \(\dfrac{1}{y}\)(công việc)
Trong 1 giờ, hai người thợ làm được: \(\dfrac{1}{16}\)(công việc)
Do đó, ta có phương trình: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{16}\)(1)
Vì khi người thứ nhất làm trong 3 giờ, người thứ 2 làm trong 6 giờ thì hoàn thành được 25% công việc nên ta có phương trình:
\(\dfrac{3}{x}+\dfrac{6}{y}=\dfrac{1}{4}\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{16}\\\dfrac{3}{x}+\dfrac{6}{y}=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{x}+\dfrac{3}{y}=\dfrac{3}{16}\\\dfrac{3}{x}+\dfrac{6}{y}=\dfrac{1}{4}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-3}{y}=\dfrac{-1}{16}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{16}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=48\\\dfrac{1}{x}=\dfrac{1}{16}-\dfrac{1}{y}=\dfrac{1}{16}-\dfrac{1}{48}=\dfrac{1}{24}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=24\\y=48\end{matrix}\right.\)(thỏa ĐK)
Vậy: Người thợ thứ nhất cần 24 giờ để hoàn thành công việc khi làm một mình
Người thợ thứ hai cần 48 giờ để hoàn thành công việc khi làm một mình
B
1 tháng 2 2021
Gọi thời gian để người thứ nhất và người thứ hai một mình hoàn thành công việc lần lượt là x (giờ) và y (giờ). (Điều kiện x, y > 16).
⇒ Trong một giờ, người thứ nhất làm được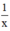 
(công việc); người thứ hai làm được 
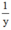(công việc).
+ Cả hai người cùng làm sẽ hoàn thành công việc trong 16 giờ nên ta có phương trình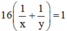 
+ Người thứ nhất làm trong 3 giờ, người thứ hai làm trong 6 giờ thì hoàn thành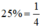 
công việc nên ta có phương trình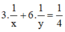 
Vậy ta có hệ phương trình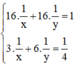 
Đặt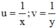 
, hệ phương trình trở thành:
22 tháng 1 2016
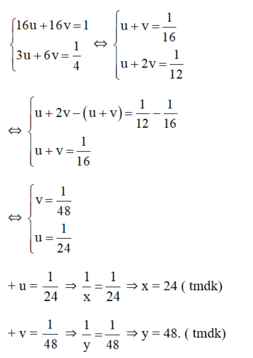
Gọi người 1 , 2 làm trong k , t ngày thì xong công việc ( k,t>0 )
Ta có hệ pt \(\int^{\frac{2}{k}+\frac{5}{t}=\frac{1}{2}}_{\frac{3}{k}+\frac{3}{t}=1-\frac{1}{20}}\)
28 tháng 1
Gọi thời gian làm riêng hoàn thành công việc của người thứ nhất và người thứ hai lần lượt là x(giờ) và y(giờ)
(Điều kiện: x>0 và y>0)
Trong 1 giờ, người thứ nhất làm được \(\dfrac{1}{x}\)(công việc)
Trong 1 giờ, người thứ hai làm được \(\dfrac{1}{y}\)(công việc)
Trong 1 giờ, hai người làm được \(\dfrac{1}{18}\)(công việc)
Do đó, ta có phương trình: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{18}\left(1\right)\)
Trong 6 giờ, người thứ nhất làm được \(6\cdot\dfrac{1}{x}=\dfrac{6}{x}\)(công việc)
Trong 12 giờ, người thứ hai làm được \(12\cdot\dfrac{1}{y}=\dfrac{12}{y}\left(côngviệc\right)\)
Nếu người thứ nhất làm trong 6 giờ và người thứ hai làm trong 12 giờ thì hai người làm được 50% công việc nên ta có:
\(\dfrac{6}{x}+\dfrac{12}{y}=\dfrac{1}{2}\left(2\right)\)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{18}\\\dfrac{6}{x}+\dfrac{12}{y}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{12}{x}+\dfrac{12}{y}=\dfrac{12}{18}=\dfrac{2}{3}\\\dfrac{6}{x}+\dfrac{12}{y}=\dfrac{1}{2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{6}{x}=\dfrac{2}{3}-\dfrac{1}{2}=\dfrac{1}{6}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{18}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=36\\y=36\end{matrix}\right.\left(nhận\right)\)
Vậy: Thời gian làm riêng hoàn thành công việc của người thứ nhất là 36 giờ
Thời gian làm riêng hoàn thành công việc của người thứ hai là 36 giờ
22 tháng 2 2022
Gọi thời gian làm riêng của người thứ nhất và người thứ hai lần lượt là x,y
Theo đề, ta có:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{40}\\\dfrac{5}{x}+\dfrac{6}{y}=\dfrac{2}{15}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{x}+\dfrac{5}{y}=\dfrac{1}{8}\\\dfrac{5}{x}+\dfrac{6}{y}=\dfrac{2}{15}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-1}{y}=\dfrac{-1}{120}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{40}\end{matrix}\right.\)
=>y=120; x=60
22 tháng 2 2022
Tham khảo:
Gọi số giờ làm riêng của người công nhân thứ I là: x (giờ) (x > 40)
Gọi số giờ làm riêng của người công nhân thứ II là: y (giờ) (y > 40)
+) Một giờ người thứ I làm được: 1/x (công việc)
Một giờ người thứ II làm được: 1/y(công việc)
Trong một giờ cả 2 người làm được: 140 (công việc)
Ta có phương trình: 1/x+ 1/y= 140(1)
+) Người thứ nhất làm trong 5h: 5/x (công việc)
Người thứ nhất làm trong 6h: 6/y (công việc)
Cả 2 người làm được: 2/15(công việc)
Ta có phương trình: 5/x+ 6/y = 2/15(2)
Từ (1)(1) và (2)(2), ta có hệ phương trình:
{1/x+1/y=1/40
5/x+6/y=215
{x=60
y=120
Vậy nếu làm riêng thì người : Thứ I mất 60 giờ để hoàn thành công việc.
Thứ II mất 120 giờ để hoàn thành công việc.
CM
6 tháng 2 2017
Gọi thời gian để người thứ nhất và người thứ hai một mình hoàn thành công việc lần lượt là x (giờ) và y (giờ). (Điều kiện x, y > 16).
⇒ Trong một giờ, người thứ nhất làm được 1/x (công việc); người thứ hai làm được 1/y (công việc).
+ Cả hai người cùng làm sẽ hoàn thành công việc trong 16 giờ nên ta có phương trình 16 1 x + 1 y = 1
+ Người thứ nhất làm trong 3 giờ, người thứ hai làm trong 6 giờ thì hoàn thành 25 % = 1 4 công việc nên ta có phương trình 3 ⋅ 1 x + 6 ⋅ 1 y = 1 4
Vậy ta có hệ phương trình 16 ⋅ 1 x + 16 ⋅ 1 y = 1 3 ⋅ 1 x + 6 ⋅ 1 y = 1 4
Đặt u = 1 x ; v = 1 y , hệ phương trình trở thành:
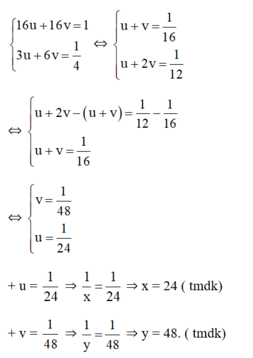
Vậy nếu làm riêng, người thứ nhất hoàn thành công việc sau 24 giờ và người thứ hai hoàn thành công việc trong 48 giờ.
Kiến thức áp dụng
Giải bài toán bằng cách lập hệ phương trình :
Bước 1 : Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp
- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn
- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.
- Từ các phương trình vừa lập rút ra được hệ phương trình.
Bước 2 : Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).
Bước 3 : Đối chiếu nghiệm với điều kiện và kết luận.
HH
2 tháng 2 2021
- Gọi x ( giờ ) là thời gian người thứ nhất hoàn thành xong công việc
- Gọi y ( giờ) là thời gian người thứ 2 hoàn thành xong công việc ( x,y > 0 )
- Trong 1h : người thứ nhất làm được \(\frac{1}{x}\)( công việc )
người thứ hai làm được \(\frac{1}{y}\)( công việc )
Ta có PT : \(\frac{1}{x}+\frac{1}{y}=\frac{1}{16}\left(1\right)\)
- Nếu người thứ nhất lúc đầu chỉ làm 3h và người thứ 2 làm trong 6h thì chỉ được 25% công việc
\(\frac{3}{x}+\frac{6}{x}=\frac{1}{4}\left(2\right)\)
- Từ (1) và (2) , ta có HPT : \(\hept{\begin{cases}\frac{1}{x}+\frac{1}{y}=\frac{1}{16}\\\frac{3}{x}+\frac{6}{y}=\frac{1}{4}\end{cases}}\)
Đặt \(\frac{1}{x}=u;\frac{1}{y}=v\), ta có :
\(\hept{\begin{cases}u+v=\frac{1}{16}\\3u+6v=\frac{1}{4}\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}6u+6v=\frac{3}{8}\\3u+6v=\frac{1}{4}\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}-3u=-\frac{1}{8}\\3u+6v=\frac{1}{4}\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}u=\frac{1}{24}\\\frac{1}{8}+6v=\frac{1}{4}\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}u=\frac{1}{4}\\6v=\frac{1}{8}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\frac{1}{x}=\frac{1}{24}\\\frac{1}{y}=\frac{1}{48}\end{cases}\Leftrightarrow\hept{\begin{cases}x=24\\y=48\end{cases}}}\)( TM )
Vậy : người thứ nhất làm xong trong 24h
người thứ 2 làm xong trong 48h
CM
2 tháng 11 2017
Gọi thời gian để người thứ nhất và người thứ hai một mình hoàn thành công việc lần lượt là x (giờ) và y (giờ). (Điều kiện x, y > 16).
⇒ Trong một giờ, người thứ nhất làm được 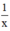(công việc); người thứ hai làm được 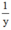(công việc).
+ Cả hai người cùng làm sẽ hoàn thành công việc trong 16 giờ nên ta có phương trình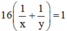
+ Người thứ nhất làm trong 3 giờ, người thứ hai làm trong 6 giờ thì hoàn thành 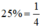công việc nên ta có phương trình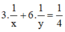
Vậy ta có hệ phương trình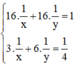
Đặt 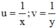, hệ phương trình trở thành:
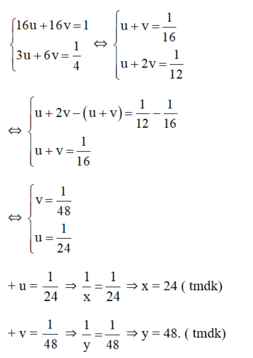
Vậy nếu làm riêng, người thứ nhất hoàn thành công việc sau 24 giờ và người thứ hai hoàn thành công việc trong 48 giờ.
Hai người cùng làm trong 1 giờ được số phần công việc là:
1:12=\(\dfrac{1}{12}\)(công việc)
Hai người cùng làm trong 4 giờ được số phần công việc là:
\(\dfrac{1}{12}\)×4=\(\dfrac{1}{3}\) (công việc)
Người thứ hai làm một mình trong 2 giờ được số phần công việc là:
\(\dfrac{2}{5}\)−\(\dfrac{1}{3}\)=\(\dfrac{1}{15}\)(công việc)
Người thứ hai làm một mình trong 1 giờ được số phần công việc là:
\(\dfrac{1}{15}\):2=\(\dfrac{1}{30}\)(công việc)
Để hoàn thành công việc người thứ hai làm trong số thời gian là:
1:\(\dfrac{1}{30}\)=30 (giờ)
Đáp số: 30 giờ