\(2^{-1}.2^n+4.2^n=9.2^5\) tìm n thuộc N
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PN
0
BN
2
11 tháng 11 2016
a)\(32^{-n}\cdot16^n=2048\)
\(\left(2^5\right)^{-n}\cdot\left(2^4\right)^n\)=2048
\(2^{-5n}\cdot2^{4n}\)=\(2^{11}\)
\(2^{-5n+4n}=2^{11}\)
\(2^{-x}=2^{11}\)
\(\Rightarrow x=-11\)
b)\(2^{-1}\cdot2^n+4\cdot2^n=9\cdot2^5\)
\(\frac{1}{2}\cdot2^n+4\cdot2^n=288\)
\(2^n\left(\frac{1}{2}+4\right)=288\)
\(2^n\cdot\frac{9}{2}=288\)
\(2^n=288:\frac{9}{2}\)
\(2^n=64\)
\(2^n=2^6\)
\(\Rightarrow n=6\)
11 tháng 11 2016
a) 32-n . 16n = 2048
\(\frac{1}{32n}\) . 16n = 2048
\(\frac{1}{2^n.16^n}\) . 16n = 2048
\(\frac{1}{2^n}\) = 2048
2-n = 2048
2-n = 211
\(\Rightarrow\) -n = 11
\(\Rightarrow\) n = -11
Vậy n = -11
AL
14 tháng 2 2021
2-1.2n+4.2n=9.25
=>2n-1+22.2n=9.25
=>2n-1+2n+2=9.25
=>2n-1.(23+1)=9.25
=>2n-1.9=9.25
=>2n-1=25
=>n-1=5=>n=6
14 tháng 2 2021
Ta có: \(2^{-1}\cdot2^n+4\cdot2^n=9\cdot2^5\)
\(\Leftrightarrow2^n\cdot2^{-1}+2^n\cdot2^2=9\cdot2^5\)
\(\Leftrightarrow2^n\cdot\left(2^{-1}+2^2\right)=9\cdot2^5\)
\(\Leftrightarrow2^n\cdot\dfrac{9}{2}=9\cdot2^5\)
\(\Leftrightarrow2^n=9\cdot2^5:\dfrac{9}{2}=2^5\cdot9\cdot\dfrac{2}{9}=2^6\)
hay n=6
Vậy: n=6
4 tháng 7 2016
\(\frac{1}{2}.2^n+4.2^n=9.2^5\)
\(2^n.\left(\frac{1}{2}.4\right)=288\)
\(2^n.2=288\)
\(2^n=288:2\)
\(2^n=144\)
Suy ra n ko tìm được
4 tháng 7 2016
Ta có :
\(\frac{1}{2}\cdot2^n+4\cdot2^n=\frac{9}{2}\cdot2^5\)
\(=>\left(\frac{1}{2}+4\right)\cdot2^n=9\cdot2^5\)
\(=>\left(\frac{1}{2}+\frac{8}{2}\right)\cdot2^n=9\cdot2^5\)
\(=>\frac{9}{2}\cdot2^n=\frac{9}{2}\cdot2^5\)
\(=>2^n=2^5\)
\(=>n=5\)
17 tháng 10 2021
\(\dfrac{1}{2}\cdot2^n+4\cdot2^n=9\cdot2^5\\ \Rightarrow2^n\left(\dfrac{1}{2}+4\right)=9\cdot2^5\\ \Rightarrow2^n\cdot\dfrac{9}{2}=9\cdot2^5\\ \Rightarrow2^{n-1}\cdot9=9\cdot2^5\\ \Rightarrow n-1=5\\ \Rightarrow n=6\)
G6
2
7 tháng 10 2018
\(2^{-1}.2^n+4.2^n=9.2^5\)
\(2^n.2=9.2^5\)
\(\Rightarrow2^n=9.2^4\)
Ko có n nhé bn
AC
1
1 tháng 7 2016
a) \(\frac{1}{9}.27^n=3^n\)
\(=>\frac{27^n}{9}=3^n\)
\(=>3^n=3^n=>n=1\)
b) \(2^{-1}.2^n+4.2^n=9.2^5\)
\(=>2^{n-1}.2^2.2^n=9.2^5\)
\(=>2^{n-1}.2^{2+n}=9.2^5\)
\(=>2^{2n+1}=9.5^2\)
\(=>n=\)
Câu b đề sai hay sao ấy số xấu lắm
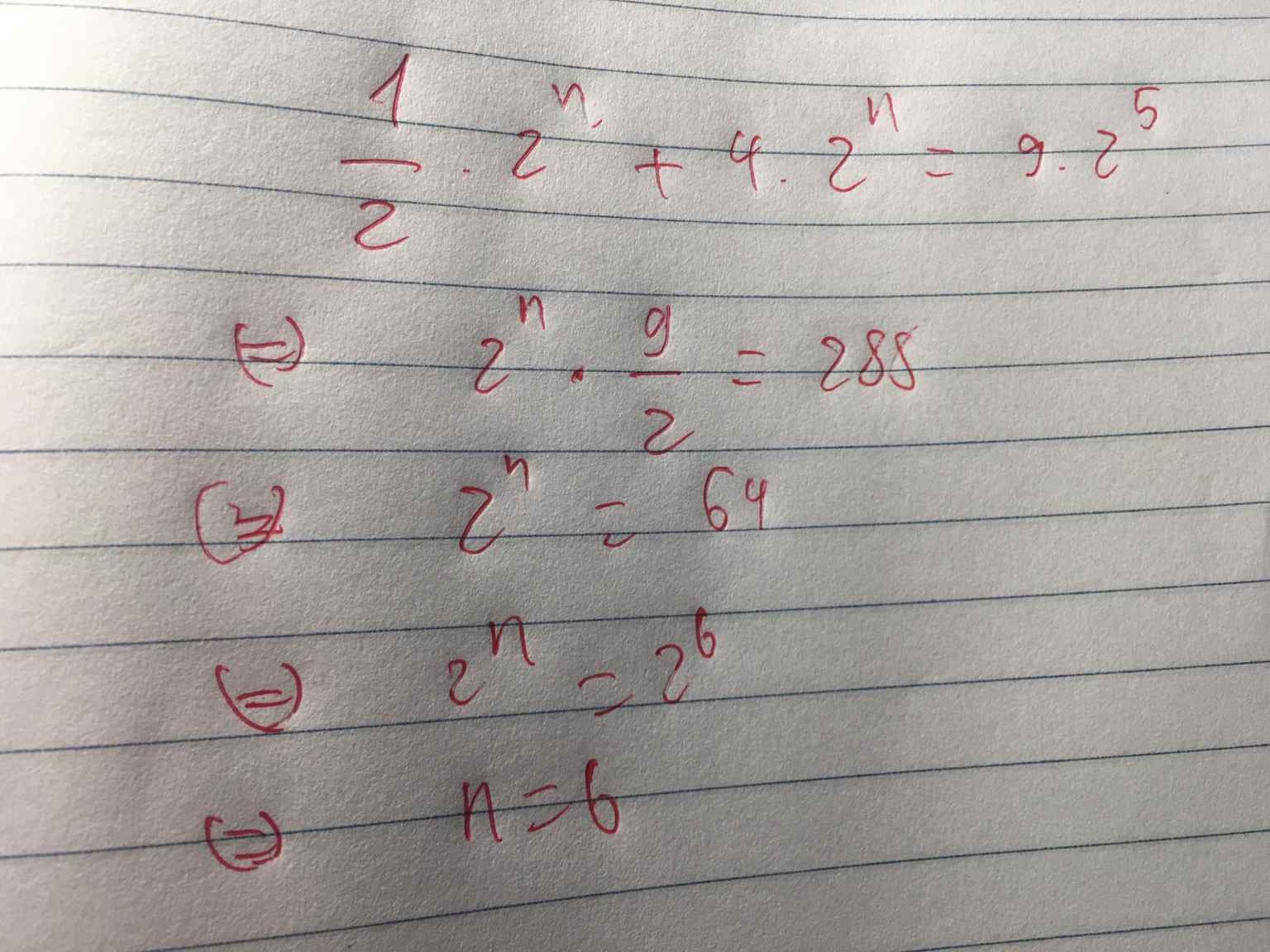
\(\Leftrightarrow2^n\left(\frac{1}{2}+4\right)=9\cdot2^5\Leftrightarrow2^n\cdot\frac{9}{2}=9\cdot2^5\Leftrightarrow2^n=2^6\Leftrightarrow n=6\)