cho đoạn thằng AB. Gọi P và Q là hai điểm phân biệt nằm giữa điểm A và B sao cho AP = QB. Gọi i là trung điểm của đoạn thằng AB. biết AB = 16 cm ; PA = 5cm. Tính BP
gấp!!! mọi người ghi cách trình bày ra giúp mình luôn nha! cảm ơn ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 8 2019
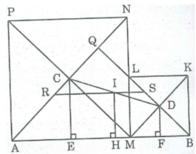
Gọi Q là giao điểm của BL và AN.
Ta có:
AN ⊥ MP (tính chất hình vuông)
BL ⊥ MK (tính chất hình vuông)
MP ⊥ MK (tính chất hình vuông)
Suy ra:
BL ⊥ AN ⇒ ∆ QAB vuông cân tại Q cố định.
M thayđổi thì I thay đổi luôn cách đoạn thẳng AB cố định một khoảng không đổi bằng a/4 nên I chuyển động trênđường thẳng song song với AB, cách AB một khoảng bằng a/4.
Khi M trùng B thì I trùng với S là trung điểm của BQ.
Khi M trùng với A thì I trùng với R là trung điểm của AQ.
Vậy khi M chuyển động trên đoạn AB thì I chuyển động trên đoạn thẳng RS song song với AB, cách AB một khoảng bằng a/4
4 tháng 12 2015
ta có C là trung điểm của A và B
suy ra AC=CB=AB/2
suy ra AC=CB= 12 cm/2
suy ra AC=CB =6cm
ta có I là trung điểm của A và B
suy ra IC=AC/2
suy ra IC=6cm/2
suy ra IC=3cm
lại có K là trung điểm của BC
suy ra CK=BC/2
suy ra CK=6cm/2
suy
ra CK=3cm
lại có BA và BC là 2 tia đối nhau
mà I thuộc BA ;K thuộc BC suy ra C nằm giữa
suy ra IC+CK=IK
thay IC=3cm;CK=3cm
suy ra IK=3cm+3cm
suy ra IK=6cm