cho M nằm ngoài (O) từ M kẻ 2 tiếp tuyến MA,MB với đường tròn, vẽ cát tuyến MCD không đi qua tâm
a)chứng minh các điểm M,A,O,B cùng thuộc một đường tròn và MO vuông góc với AB tại H
b) chứng minh MA.AD=MD.AC
c) gọi I là trung điểm của CD và E là giao điểm của AB và OI. chứng minh rằng: tứ giác OECH nội tiếp

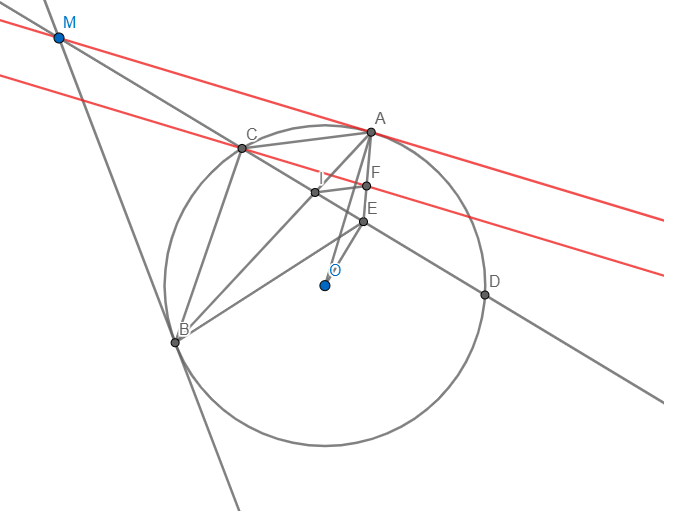
cần gấp câu c) ạ