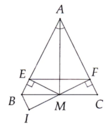
cho tam giác ABC cân tại A ,Tia phân giác của góc BAC cắt cạnh BC tại M .
a) chứng minh tam giác AMB =tam giác AMC
b)Vẽ ME vuông góc với AB ( E thuộc AB);MF vuông góc với AC(F thuộc AC) .Chứng minh tam giác MEF cân
c) Chứng minh AM vuông góc với EF
d) Vẽ EI vuông góc BC tại I.Gọi K là giao điểm của đường thẳng EI và AC. chứng minh A là trung điểm của KF

a: Xét ΔAMB và ΔAMC có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó:ΔAMB=ΔAMC
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó:ΔAEM=ΔAFM
Suy ra:ME=MF
hay ΔMEF cân tại M
c: Ta có: AE=AF
ME=MF
Do đó: AM là đường trung trực của FE
hay AM⊥FE