Cho tam giác ABC nhọn có đường cao là BD và CE cắt nhau tại I .CMR góc BIC bù với góc A
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 5 2017
a) Có góc A chung và 2 góc vuông => ĐPCM
b) Xét EHB và DHC có:
2 góc vuông và 2 góc đối đỉnh EHB và DHC
=> EHB đồng dạng với DHC
=>BH/CH=EH/DH
=>BH.DH=EH.CH
c)Từ câu a ta suy ra được tỉ số : AB/AC=AD/AE
và có góc A chung .
Từ đó suy ra: ADE đồng dạng với ABC
=> góc ADE= góc ABC
d) Ta có IO là đường trung bình ( tự chứng minh )
=> IO//AH => AHM đồng dạng với IOM
Tỉ số cạnh = AM/IM =2 ( do là đường trung bình )
Tỉ số diện tích của AHM so với IOM là 22=4
Vậy SAHM=4.SIOM
19 tháng 8 2017
A B C D E F I 1 2 3 4
a) xét tg BEF có: BD là pg của ^B (gt) và EF vg vs BD (gt)
=> tg BEF cân tại B=> BD cx là đg trung trực ứng vs cạnh EF => E đx vs F qua BD
b)ta có: ^ BAC +^ ABC +^ACB=180( t/c tổng các goác trong tg)
=>60+ 2 ^IBC +2.^ICB=180 (vì ^ BAC=60 )
=> ^IBC+^ICB=60
xét tg IBC có: ^BIC +^ICB +^IBC =180 (t/c tổng các góc trong tg)
=> ^BIC= 120 (vì ^IBC +^ICB =60)
Mà ^BIC +\(^{\widehat{I}_1}\)=180 (vì 2 góc này bù nhau) =>\(^{\widehat{I}_1}\) =60 (vì ^BIC=120)
^BIC +\(\widehat{I_4}\)=180(vì.........................)=>\(\widehat{I_4}\)=60
=> \(^{\widehat{I}_1}\)= \(\widehat{I_2}\)=60 (vì 2 góc này đối xứng vs nhau)
và \(\widehat{I_4}\) = \(\widehat{I_3}\)=60(vì ...................................)
=>\(\widehat{I_2}\) =\(\widehat{I_3}\) =60 => IF là tia pg của ^BIC
c)xét tg IDC và tg IFC có: \(\widehat{I_4}\)= \(\widehat{I_3}\) (=60) ; IC chung ; ^DCI=^FCI (vì IC là pg của ^C)
=>tg IDC =tg IFC (g.c.g)
=> ID=IF và DC=FC => IC là đg trung trực của DF => D đx vs F qua IC
23 tháng 4 2016
vẽ hình
a xét tam giác ABD và tam giác ACE có :
chung góc BAC
góc BDA = góc CEA = 90 độ
=> tam giác ABD đồng dạng tam giác ACE (g.g)
b, xét tam giác EHB và tam giác DHC có
góc BDC = góc CFB = 90 độ
góc BHF = góc DHC ( đối đỉnh )
=> tam giác EHB đồng dạng với tam giác DHC (g.g)
=> \(\frac{HB}{HC}=\frac{HE}{HD}\)
=> HD . HB = HE . HC ( đpcm )
c, vì tam giác ABD đồng dạng với tam giác ACE ( câu a)
=> \(\frac{AB}{AC}=\frac{AD}{AE}\) => \(\frac{AE}{AC}=\frac{AD}{AB}\)
xét tam giác ADE và tam giác ABC có
chung góc BAC
\(\frac{AE}{AC}=\frac{AD}{AB}\)
=> tam giác ADE đồng dạng với tam giác ABC ( c.g.c)
=> góc ADE = góc ABC ( đpcm)
HD
22 tháng 8 2022
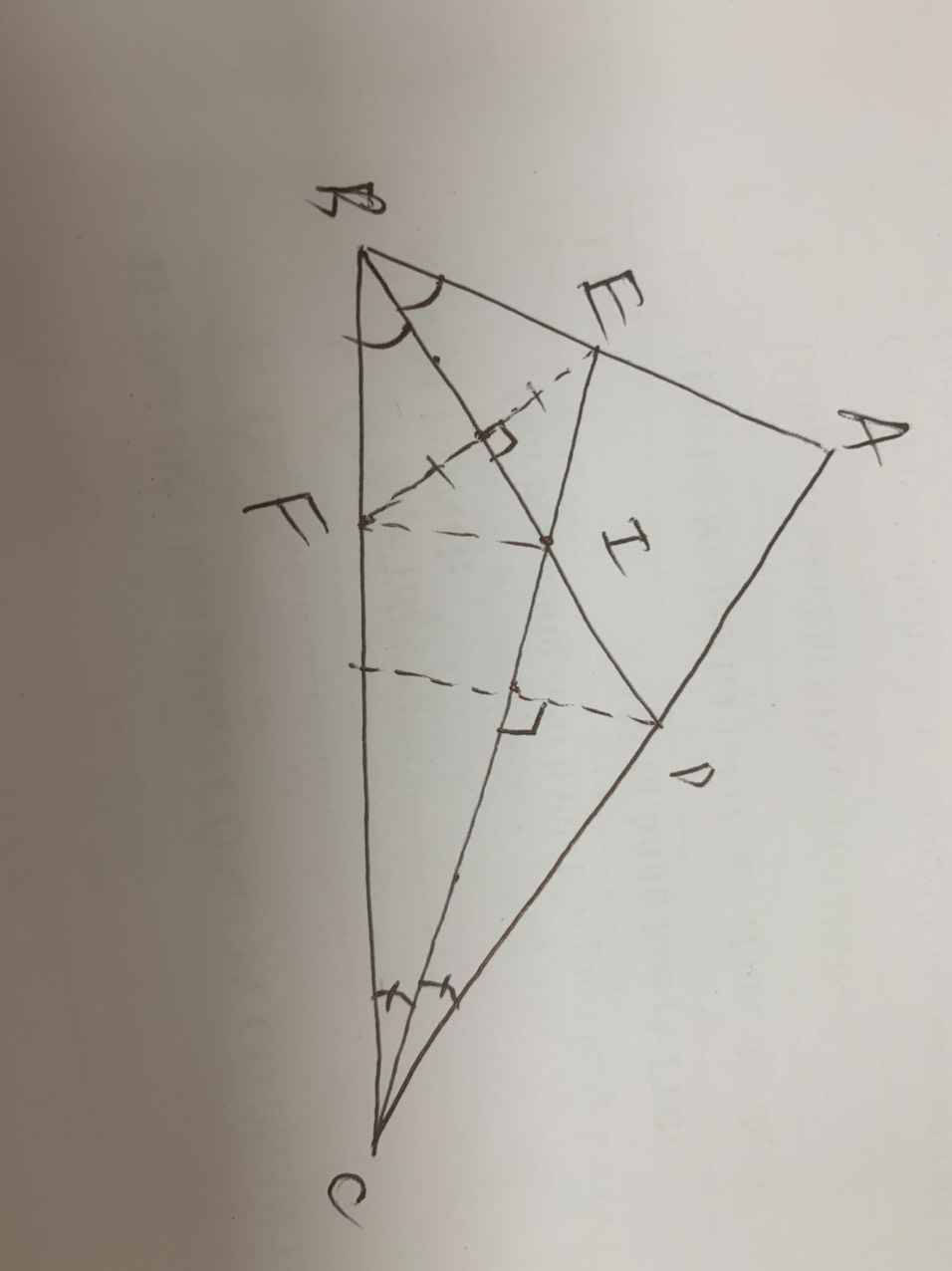Với đề bài cho như bạn viết thì câu a thì chứng minh đúng được. Còn câu b thì IF không thể là phân giác của góc BCI được. Câu c là F không thể đối xứng được D qua CI (hình vẽ minh hoạ, luôn tồn tại điểm K trên BC khác điển F)
