Cho tam giác ABC có ba góc nhọn và ba cạnh không bằng nhau. Kẻ hai đường cao AH vàBM cắt nhau tại P. Phân giác trong CL cắt AH và BM theo thứ tự ở Q và R. chứng minh rằng tam giác PQR là tam giác cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 7 2023
a: góc INC+góc IMC=180 độ
=>INCM nội tiếp
b: Xét ΔINB vuông tại N và ΔIMA vuông tại M có
góc NIB=góc MIA
=>ΔINB đồng dạng với ΔIMA
=>IN/IM=IB/IA
=>IN*IA=IM*IB
c: góc AIH=góc BIN=góc BCA
=>góc AIH=góc AHI
=>AI=AH
27 tháng 7 2023
a: góc INC+góc IMC=90+90=180 độ
=>IMCN nội tiếp
b: Xét ΔIMA vuông tại M và ΔINB vuông tại N có
góc MIA=góc NIB
=>ΔIMA đồng dạng với ΔINB
=>IM/IN=IA/IB
=>IM*IB=IN*IA
c: góc AHI=góc ACB
=>góc AHI=góc AIH
=>AH=AI
27 tháng 7 2023
a: góc INC+góc IMC=90+90=180 độ
=>IMCN nội tiếp
b: Xét ΔIMA vuông tại M và ΔINB vuông tại N có
góc MIA=góc NIB
=>ΔIMA đồng dạng với ΔINB
=>IM/IN=IA/IB
=>IM*IB=IN*IA
c: góc AHI=góc ACB
=>góc AHI=góc AIH
=>AH=AI
HM
21 tháng 6 2017
.
GIẢ SỬ TAM GIÁC PQR LÀ TAM GIÁC ĐỀU
TA CÓ GÓC PRQ = 60
=> GÓC BMC + GÓC ACB = 120
=> GÓC BMC + GÓC \(\frac{ACB}{2}=120\)
=> GÓC BMC = \(120-\frac{ACB}{2}\)
NỐI HM
DO HM LÀ ĐƯỞNG TRUNG TUYẾN ỨNG VỚI CẠNH HUYỀN CỦA TAN GIÁC AHC VUÔNG TAI H
=> MH = AM = MC
=> GÓC HMC = 180 - 2 . GÓC ACB VÀ GÓC MHA = GÓC HAC = 90 - GÓC ACB
=> GÓC BMH = GÓC BMC - GÓC HMC = \(120-\frac{ACB}{2}-180+2.ACB\)
DO GÓC QPR = 60
=> GÓC MHA + GÓC BMH = 120
=> 90 - GÓC ACB + 120 - \(\frac{ACB}{2}-180+2.ACB=120\)
=> 30 + \(\frac{ACB}{2}=120\)
=> GÓC ACB = 90 . 2 = 180 ( VÔ LÍ )
VẬY TAM GIÁC PQR KHÔNG THỂ LÀ TAM GIÁC ĐỀU
29 tháng 7 2017
Cách 2:
Giả sử \(\Delta\)PQR là tam giác đều \(\Rightarrow\)^QPR=^PRQ=^PQR=600.
Xét \(\Delta\)PHC: ^PHC=900 \(\Rightarrow\)^C2=900-^QPR=300
Do CL là phân giác trong của ^ACB \(\Rightarrow\)^C1=^C2=300\(\Rightarrow\)^ACB=600 (1)
Ta có: ^PRQ=^MRC=600 (Đối đỉnh).
Xét \(\Delta\)RMC: ^RMC=1800-(^MRC+^C1)=1800-900=900 \(\Rightarrow\)RM\(⊥\)AC hay BM\(⊥\)AC
\(\Rightarrow\)BM là đường trung tuyến đồng thời là đường cao của \(\Delta\)ABC\(\Rightarrow\)\(\Delta\)ABC cân tại B (2)
Từ (1) và (2) \(\Rightarrow\)\(\Delta\)ABC đều \(\Rightarrow\)AB=BC=AC (Mâu thuẫn với đề bài)
\(\Rightarrow\)Giả sử là Sai. Vậy nên \(\Delta\)PQR không thể là tam giác đều.
31 tháng 7 2023
a: góc BHD+góc BMD=180 độ
=>BHDM nội tiếp
b: BHDM nội tiếp
=>góc HDM+góc HBM=180 độ
=>góc ADM=góc ABC
=>góc ADM=góc ADC
=>DA là phân giáccủa góc MDC
c: Xét tứ giác DHNC có
góc DHC=góc DNC=90 độ
=>DHNC nội tiếp
=>góc NHD=góc NDC
góc NHD+góc MHD
=180 độ-góc NCD+góc MBD
=180 độ+180 độ-góc ABD-góc ACD
=180 độ
=>M,H,N thẳng hàng
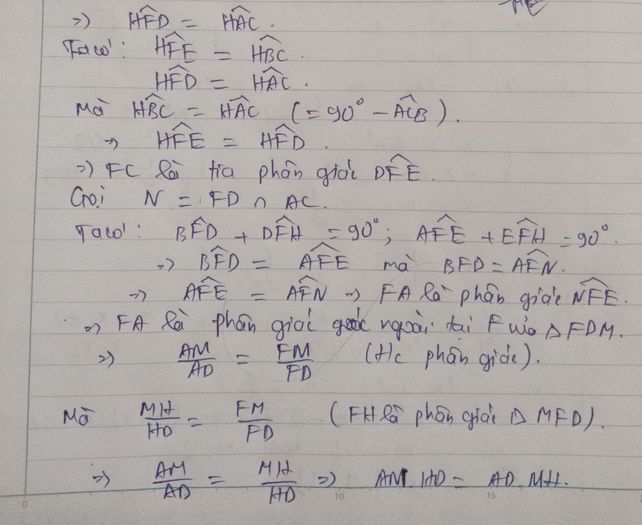Bạn tham khảo cách làm nhé!