Bài 2. Cho tam giác ABC vuông tại A, AB = 12cm, AC = 16cm. Tia phân giác góc A cắt BC tại D.
a) Tính độ dài các đoạn thẳng BD, CD.
b) Từ D kẻ DE vuông góc với AC (E thuộc AC). Tính DE, AD.
Bài 3. Cho hình bình hành ABCD có CD = 4cm. Kẻ AH vuông góc với DC (H thuộc DC). Biết AH = 3cm.
a) Tính diện tích hình bình hành ABCD.
b) Gọi M là trung điểm AB, DM cắt AC tại N. Chứng minh: DN = 2NM.
c) Tính diện tích tam giác AMN.




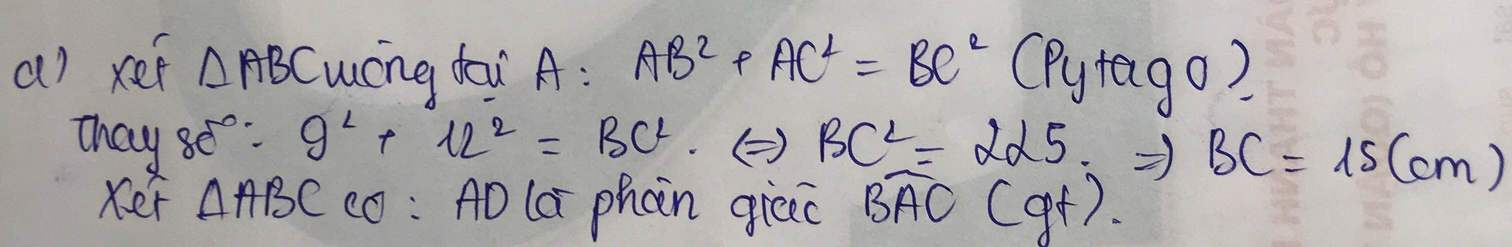
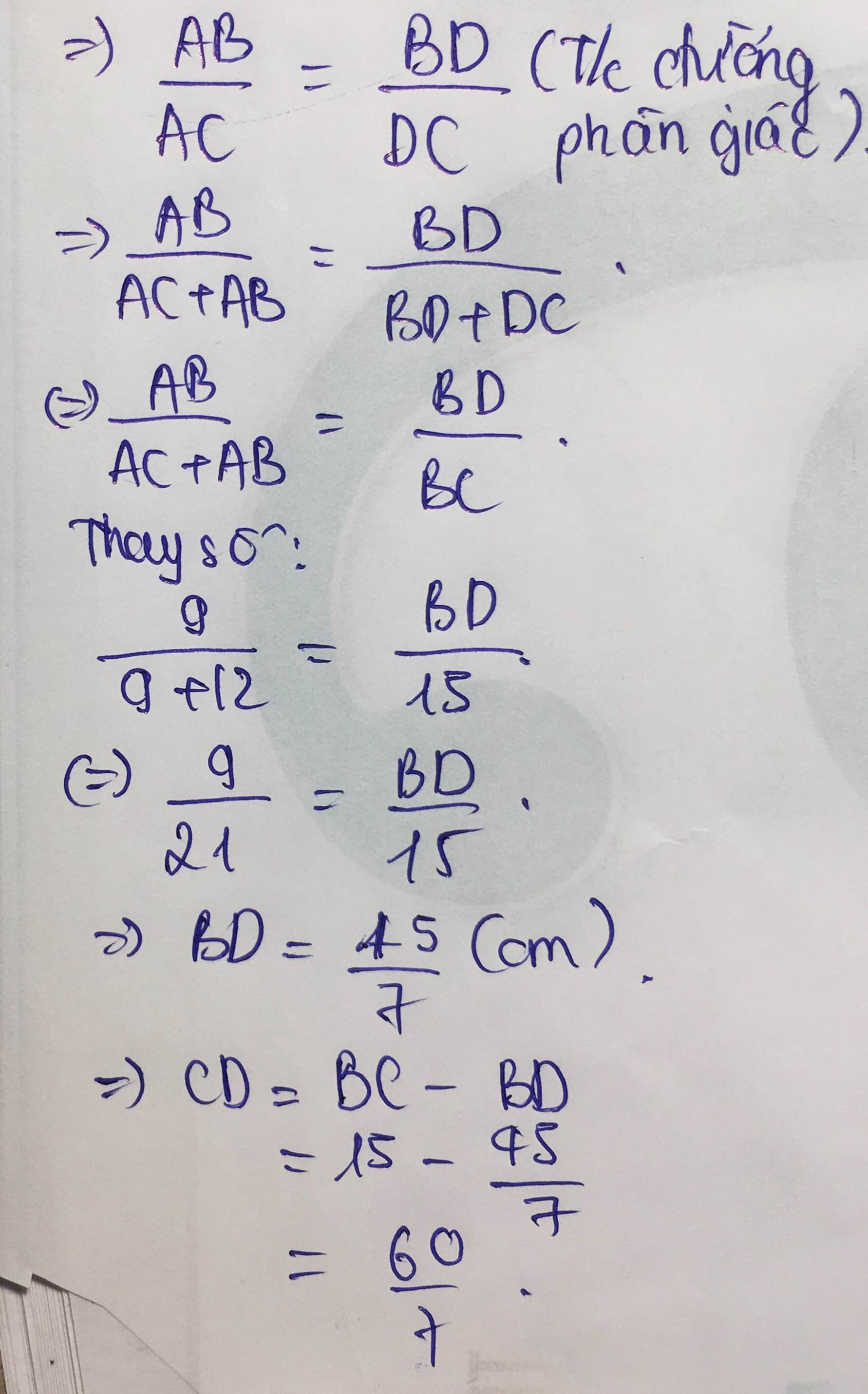
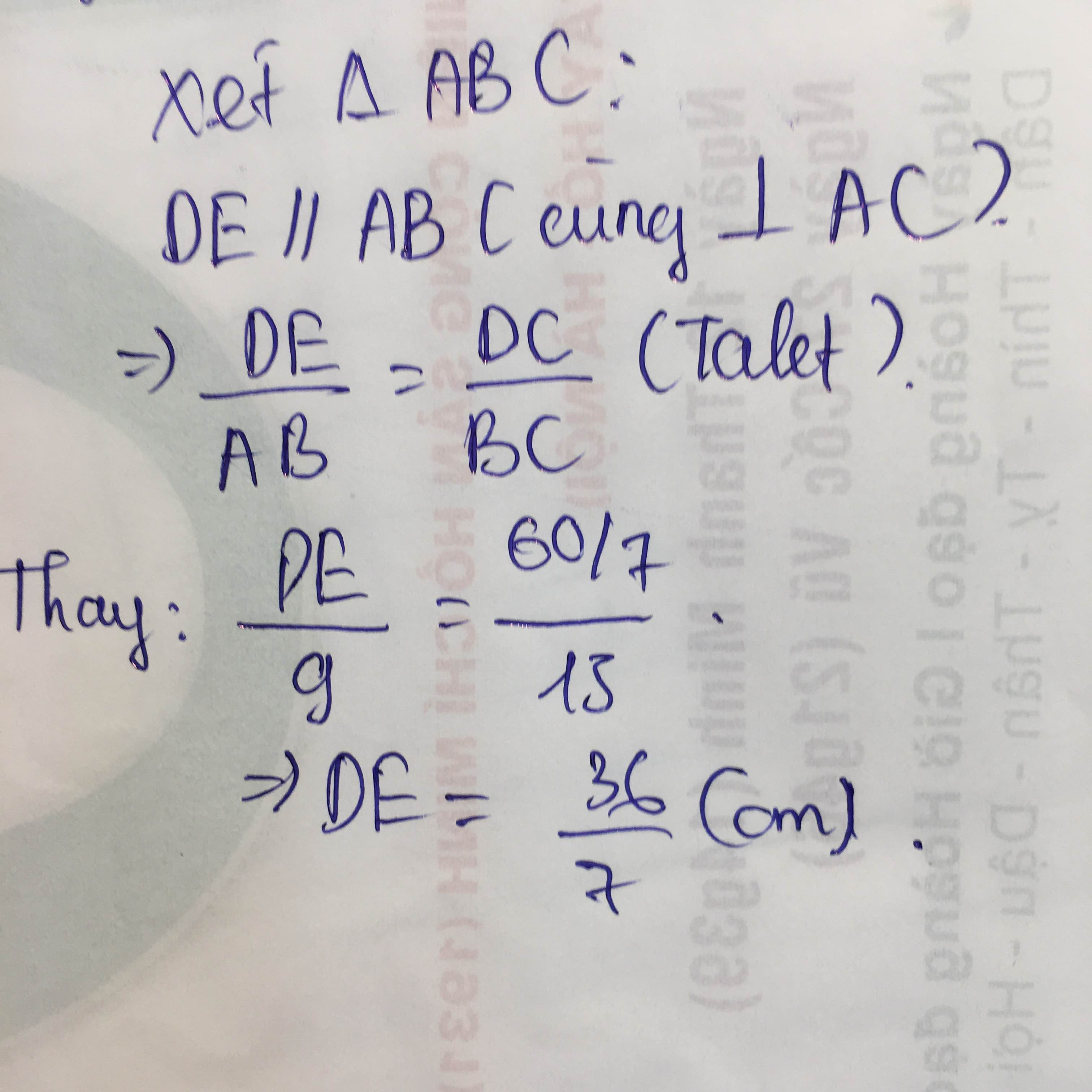
Bài 2:
a:
BC=20cm
Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/12=CD/16
=>BD/3=CD/4
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{20}{7}\)
Do đó: BD=60/7(cm); CD=80/7(cm)
b: Xét ΔABC có DE//AB
nên DE/AB=CD/BC
=>DE/12=4/7
hay DE=48/7(cm)