(3x-1)^2=9(x-2)(x+1)+38
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 3 2021
a) \(\left(3x+2\right)^2-\left(3x-2\right)^2=5x+38\)
\(\Leftrightarrow\left[\left(3x+2\right)-\left(3x-2\right)\right]\left[\left(3x+2\right)+\left(3x-2\right)\right]=5x+38\)
\(\Leftrightarrow\left(3x+2-3x+2\right)\left(3x+2+3x-2\right)=5x+38\)
\(\Leftrightarrow4\cdot6x=5x+38\)
\(\Leftrightarrow24x-5x=38\)
\(\Leftrightarrow19x=38\Leftrightarrow x=\dfrac{38}{19}=2\)
Vậy \(S=\left\{2\right\}\)
b) \(\left(x+1\right)\left(x^2-2x+1\right)-2x=2\left(x-1\right)\left(x+1\right)\)
\(\Leftrightarrow x^3-2x^2+x+x^2-2x+1-2x=2\left(x^2-1\right)\)
\(\Leftrightarrow x^3-2x^2+x+x^2-2x+1-2x=2x^2-2\)
\(\Leftrightarrow x^3-2x^2+x+x^2-2x+1-2x-2x^2+2=0\)
\(\Leftrightarrow x^3-3x^2-3x+3=0\)
PT vô nghiệm , không tìm được x
Vậy \(S=\varnothing\)
c) \(3\left(x-2\right)^2+9\left(x-1\right)=3\left(x^2+x-3\right)\)
\(\Leftrightarrow3\left(x^2-2x+4\right)+9\left(x-1\right)=3\left(x^2+x-3\right)\)
\(\Leftrightarrow3x^2-6x+12+9x-9=3x^2+3x-9\)
\(\Leftrightarrow3x^2-6x+12+9x-9-3x^2-3x+9=0\)
\(\Leftrightarrow0x+12=0\)
PT vô nghiệm
Vậy \(S=\varnothing\)
Câu cuối tương tự
11 tháng 3 2023
a: =>9x^2+12x+4-9x^2+12x-4=5x+38
=>24x=5x+38
=>19x=38
=>x=2
b: =>3x^2-12x+12+9x-9=3x^2+3x-9
=>-3x+3=3x-9
=>-6x=-12
=>x=2
11 tháng 3 2023
a: =>9x^2+12x+4-9x^2+12x-4=5x+38
=>24x=5x+38
=>19x=38
=>x=2
e: =>x^3+1-2x=x^3-x
=>-2x+1=-x
=>-x=-1
=>x=1
f: =>x^3-6x^2+12x-8+9x^2-1=x^3+3x^2+3x+1
=>12x-9=3x+1
=>9x=10
=>x=10/9
b: \(\Leftrightarrow3x^2-12x+12+9x-9=3x^2+3x-9\)
=>-3x+3=3x-9
=>-6x=-12
=>x=2
AH
Akai Haruma
Giáo viên
10 tháng 1
Lời giải:
a. $(3x+9)^{40}=49(3x+9)^{38}$
$(3x+9)^{40}-49(3x+9)^{38}$
$(3x+9)^{38}[(3x+9)^2-49]=0$
$\Rightarrow (3x+9)^{38}=0$ hoặc $(3x+9)^2-49=0$
Nếu $(3x+9)^{38}=0$
$\Rightarrow 3x+9=0$
$\Rightarrow x=-3$
Nếu $(3x+9)^2-49=0$
$\Rightarrow (3x+9)^2=49=7^2=(-7)^2$
$\Rightarrow 3x+9=7$ hoặc $3x+9=-7$
$\Rightarrow x=\frac{-2}{3}$ hoặc $x=\frac{-16}{3}$
AH
Akai Haruma
Giáo viên
10 tháng 1
b/
Xét $A=2^x+2^{x+1}+2^{x+2}+....+2^{x+2015}$
$2A=2^{x+1}+2^{x+2}+2^{x+3}+....+2^{x+2016}$
$\Rightarrow 2A-A=(2^{x+1}+2^{x+2}+2^{x+3}+....+2^{x+2016})-(2^x+2^{x+1}+2^{x+2}+....+2^{x+2015})$
$\Rightarrow A=2^{x+2016}-2^x$
Vậy $2^{x+2016}-2^x=2^{2019}-8$
$\Rightarrow 2^x(2^{2016}-1)=2^3(2^{2016}-1)$
$\Rightarrow 2^x=2^3$
$\Rightarrow x=3$
6 tháng 1 2022
e: =>-40+3+33+40-x=47
=>36-x=47
=>x=-11
f: =>x(x-3)(11-x)(11+x)=0
hay \(x\in\left\{0;3;11;-11\right\}\)
g: =>-62-38-x+2x=-100
=>x-100=-100
hay x=0
6 tháng 1 2022
i: =>x-12-2x-31=6
=>-x-43=6
=>x+43=-6
hay x=-49
h: =>(x+1)=0
=>x=-1
f: =>x(x-3)(x+11)(x-11)=0
hay \(x\in\left\{0;3;-11;11\right\}\)
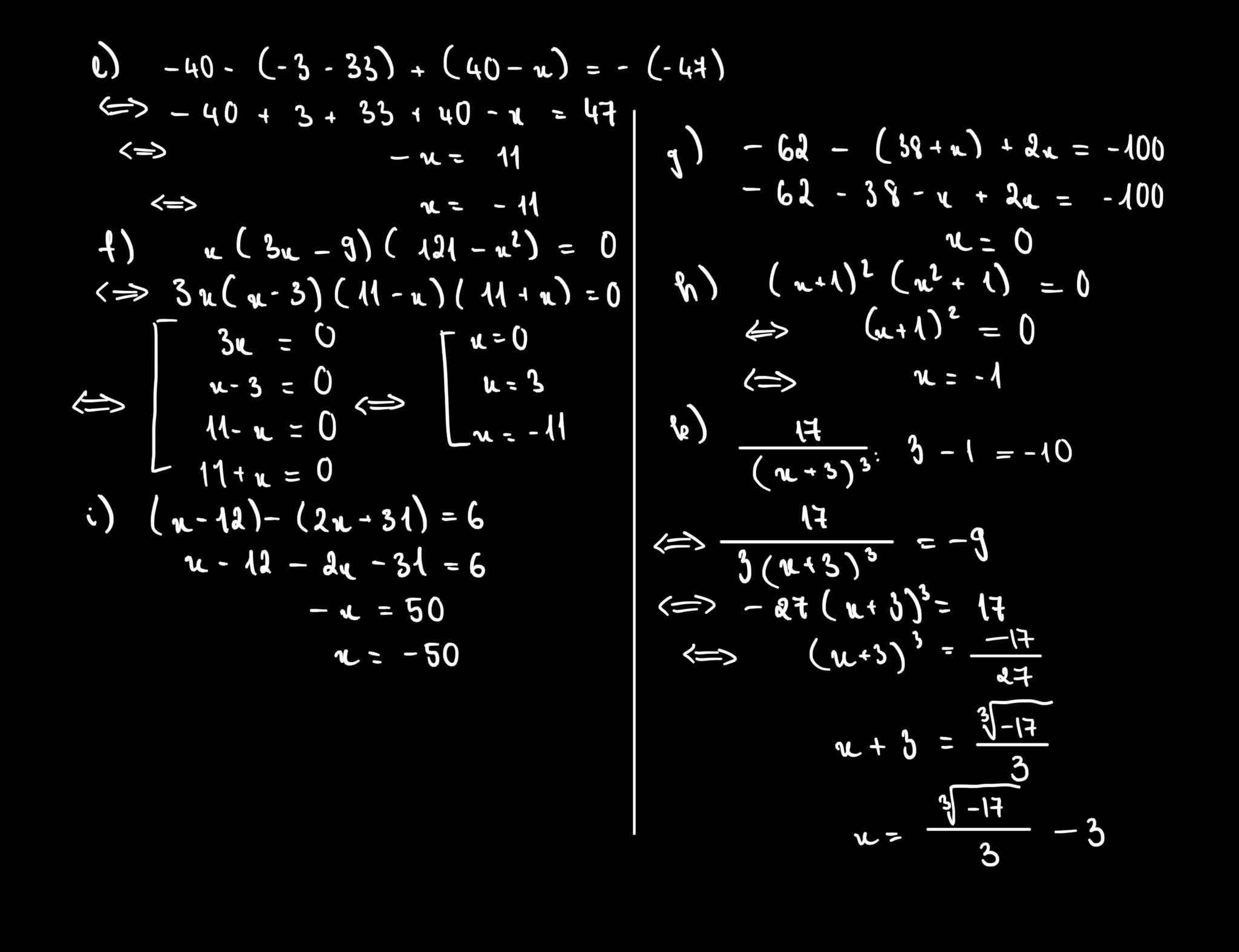
\(9x^2-6x+1=9\left(x^2-x-2\right)+38\)
\(\Leftrightarrow-6x+1=-9x+20\Leftrightarrow3x=19\Leftrightarrow x=\dfrac{19}{3}\)
`Answer:`
`(3x-1)^2=9(x-2)(x+1)+38`
`<=>9x^2-6x+1=9(x^2+x-2x-2)+38`
`<=>9x^2-6x+1=9x^2-9x-18+38`
`<=>9x^2-9x^2-6x+9x=-18+38-1`
`<=>3x=19`
`<=>x=\frac{19}{3}`