CHO TAM GIÁC MNI, P VÀ Q LẦN LƯỢT LÀ TRUNG ĐIỂM CỦA CẠNH MN VÀ MI . NQ VÀ IP CẮT NHAU TẠI G . MG CẮT CẠNH NI TẠI K. HÃY CHỨNG TỎ K LÀ TRUNG ĐIỂM CỦA NI ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Xét ΔABC có
N là trung điểm của AB(gt)
M là trung điểm của AC(gt)
Do đó: NM là đường trung bình của ΔABC
Suy ra: NM//BC và \(NM=\dfrac{BC}{2}\)(1)
Xét ΔGBC có
E là trung điểm của GB
F là trung điểm của GC
Do đó: EF là đường trung bình của ΔGBC
Suy ra: EF//BC và \(EF=\dfrac{BC}{2}\)(2)
Từ (1) và (2) suy ra NM//EF và NM=EF
hay MNEF là hình bình hành
b) Xét ΔABC có
BM là đường trung tuyến ứng với cạnh AC
CN là đường trung tuyến ứng với cạnh AB
BM cắt CN tại G
Do đó: G là trọng tâm của ΔABC
Xét ΔABC có
G là trọng tâm của ΔABC
BM là đường trung tuyến ứng với cạnh AC
Do đó: \(GB=2GM\)
mà GF=2GM
nên GB=GF
hay G là trung điểm của BF
Xét ΔABC có
G là trọng tâm của ΔABC
CN là đường trung tuyến ứng với cạnh AB
Do đó: \(GC=2GN\)
mà GI=2GN
nên GC=GI
hay G là trung điểm của CI
Xét tứ giác BIFC có
G là trung điểm của đường chéo CI(cmt)
G là trung điểm của đường chéo BF(cmt)
Do đó: BIFC là hình bình hành

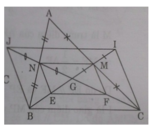
a) Ta có MN là đường trung bình của ΔABC
⇒ MN // BC và MN = BC/2
Tương tự EF là đường trung bình của ΔBGC nên EF // BC và EF = BC/2
Do đó MN // EF và MN = EF.
Vậy MNEF là hình bình hành (hai cạnh đối vừa song song vừa bằng nhau)
b) Ta có G là trong tâm của ΔABC nên GN = GC/2
Mà GN = JN (gt) ⇒ GJ = GC.
Tương tự ta có GI = GB
Vậy tứ giác BJIC là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường).

a: Xét ΔDEC có
I là trung điểm của DE
N là trung điểm của DC
Do đó: NI là đường trung bình của ΔDEC
Suy ra: \(NI=\dfrac{EC}{2}\)
hay \(NI=\dfrac{BD}{2}\left(1\right)\)
Xét ΔDBC có
N là trung điểm của DC
M là trung điểm của BC
Do đó: NM là đường trung bình của ΔDCB
Suy ra: \(NM=\dfrac{DB}{2}\left(2\right)\)
Từ (1) và (2) suy ra NI=NM
Xét ΔNIM có NI=NM
nên ΔNIM cân tại N

a) Vì BM là trung tuyến AC
=> M là trung điểm AC (1)
Vì CN là trung tuyến AB
=> N là trung tuyến AB (2)
Từ (1) và (2) => MN là đường trung bình ∆ABC
=> MN //BC , MN = \(\frac{1}{2}BC\)
Vì E là trung điểm GB
F là trung điểm GC
=> FE là đường trung bình ∆GBC
=> FE//BC
=> FE = \(\frac{1}{2}BC\)
=> NM //FE
=> FE= NM
=> NMFE là hình bình hành

4) Gọi P, Q lần lượt là tâm của các đường tròn ngoại tiếp tam giác MBK, tam giác MCK và E là trung điểm của đoạn PQ. Vẽ đường kính ND của đường tròn (O) . Chứng minh ba điểm D, E, K thẳng hàng.

Vì N là điểm chính giữa cung nhỏ BC nên DN là trung trực của BC nên DN là phân giác B D C ^
Ta có K Q C ^ = 2 K M C ^ (góc nọi tiếp bằng nửa góc ở tâm trong dường tròn (Q))
N D C ^ = K M C ^ (góc nội tiếp cùng chắn cung N C ⏜ )
Mà B D C ^ = 2 N D C ^ ⇒ K Q C ^ = B D C ^
Xét 2 tam giác BDC & KQC là các các tam giác vuông tại D và Q có hai góc ở ⇒ B C D ^ = B C Q ^ do vậy D, Q, C thẳng hàng nên KQ//PK
Chứng minh tương tự ta có ta có D, P, B thẳng hàng và DQ//PK
Do đó tứ giác PDQK là hình bình hành nên E là trung điểm của PQ cũng là trung điểm của DK. Vậy D, E, K thẳng hàng (điều phải chứng minh).

có ˆAME=ˆEHBAME^=EHB^ ( do MEHB nội tiếp)
ˆEHB=ˆENCEHB^=ENC^ ( HENC nội tiếp)
⇒ˆAME=ˆENC⇒AME^=ENC^
Vậy AMEN nội tiếp
Ta có M, N là trung điểm AB, AC nên MN song song BC nên
ˆNMH=ˆMHBNMH^=MHB^ ( MN song song BC)
ˆMHB=ˆMBHMHB^=MBH^ ( tam giác BMH cân ở M)
nênˆMBHˆNMHMBH^NMH^
mà ˆMBHMBH^ bằng nữa số đo cung MH nên $\widehat{NMH} bằng nữa số đo cung MH
vậy $\widehat{NMH} là góc tạo bởi tiếp tuyến bởi dây cung. suy ra MN là tiếp tuyến của (MBH)
Tương tự MN là tiếp tuyến của (NHC)
Gọi K là giao điểm của EH và MN
Ta có MK2=KE.KHMK2=KE.KH
NK2=KE.KHNK2=KE.KH
suy ra MK=KN. có nghĩa là HE đi qua trung điểm MN