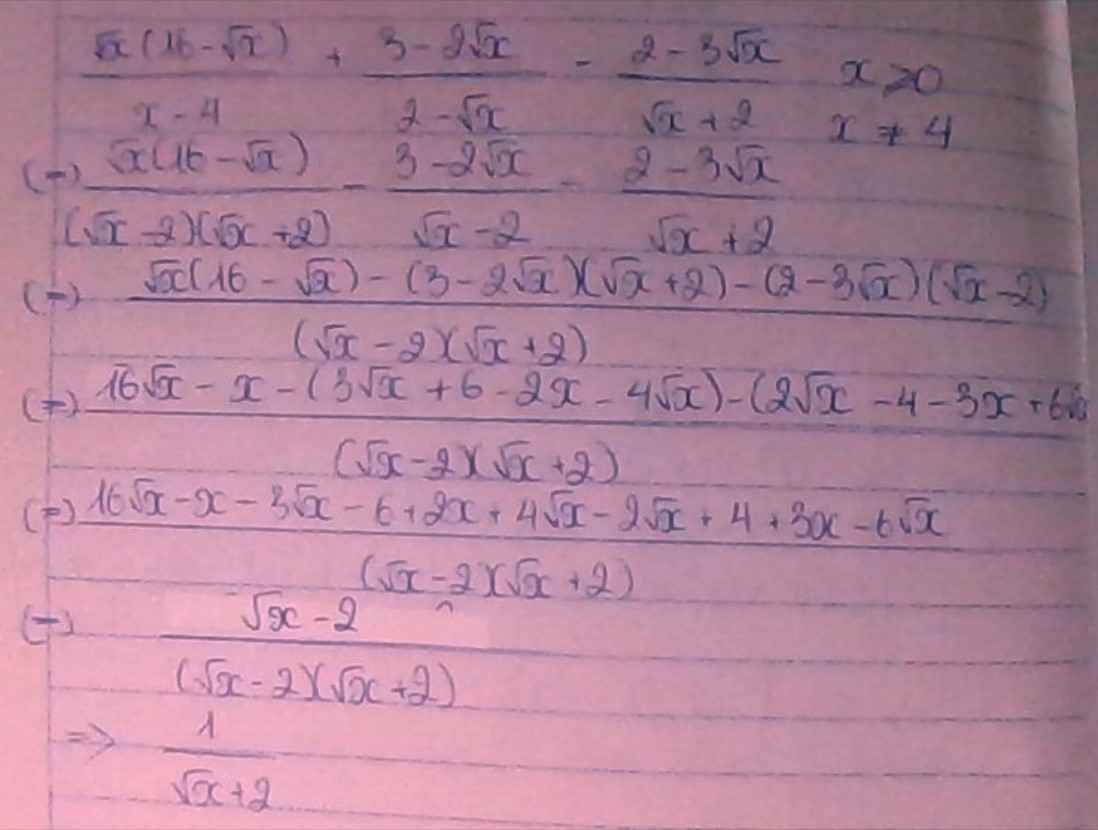Rút gọn: A=\(\sqrt{16x}+2\sqrt{40x}-3\sqrt{90x}\)với \(x\ge0\)cám ơn mấy anh chị
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
G
12 tháng 5 2017
\(A=\left(\frac{\sqrt{x}}{\sqrt{x}+3}+\frac{x+9}{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}\right).\frac{\sqrt{x}\left(\sqrt{x}-3\right)}{2\left(\sqrt{x}+2\right)}\)
\(=\frac{\sqrt{x}\left(3-\sqrt{x}\right)+x+9}{\left(3+\sqrt{x}\right)\left(3-\sqrt{x}\right)}.\frac{\sqrt{x}\left(\sqrt{x}-3\right)}{2\left(\sqrt{x}+2\right)}\)
\(=\frac{3\sqrt{x}-x+x+9}{\left(3+\sqrt{x}\right)\left(3-\sqrt{x}\right)}.\frac{\sqrt{x}\left(\sqrt{x}-3\right)}{2\left(\sqrt{x}+2\right)}\)
\(=\frac{3\left(\sqrt{x}+3\right)}{\left(3+\sqrt{x}\right)\left(3-\sqrt{x}\right)}.\frac{-\sqrt{x}\left(3-\sqrt{x}\right)}{2\left(\sqrt{x}+2\right)}\)
\(=\frac{-3\sqrt{x}}{2\left(\sqrt{x}+2\right)}\)
11 tháng 8 2021
Ta có: \(\dfrac{\sqrt{x}\left(16-\sqrt{x}\right)}{x-4}+\dfrac{3+2\sqrt{x}}{2-\sqrt{x}}-\dfrac{2-3\sqrt{x}}{\sqrt{x}+2}\)
\(=\dfrac{16\sqrt{x}-x-\left(3+2\sqrt{x}\right)\left(\sqrt{x}+2\right)+\left(3\sqrt{x}-2\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{16\sqrt{x}-x-3\sqrt{x}-6-2x-4\sqrt{x}+3x-6\sqrt{x}-2\sqrt{x}+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{1}{\sqrt{x}+2}\)
17 tháng 10 2021
\(a,A=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3\sqrt{x}-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}:\dfrac{2\sqrt{x}-2-\sqrt{x}+3}{\sqrt{x}-3}\\ A=\dfrac{x-6\sqrt{x}-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}=\dfrac{x-6\sqrt{x}-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}+1\right)}\)
10 tháng 7 2021
a) Ta có: \(\dfrac{6}{\sqrt{5}+1}+\sqrt{\dfrac{2}{3-\sqrt{5}}}-\dfrac{10}{\sqrt{5}}\)
\(=\dfrac{6\left(\sqrt{5}-1\right)}{4}+\sqrt{\dfrac{2\left(3+\sqrt{5}\right)}{4}}-2\sqrt{5}\)
\(=\dfrac{3}{2}\left(\sqrt{5}-1\right)+\dfrac{\sqrt{3+\sqrt{5}}}{\sqrt{2}}-2\sqrt{5}\)
\(=\dfrac{3}{2}\sqrt{5}-\dfrac{3}{2}-2\sqrt{5}+\dfrac{\sqrt{5}+1}{2}\)
\(=-\dfrac{1}{2}\sqrt{5}-\dfrac{3}{2}+\dfrac{1}{2}\sqrt{5}+\dfrac{1}{2}\)
=-1
10 tháng 7 2021
Bài 1:
a) Thay \(x=\dfrac{1}{4}\)vào B, ta được:
\(B=1:\left(\dfrac{1}{4}\cdot\dfrac{1}{2}+27\right)=1:\left(27+\dfrac{1}{8}\right)=\dfrac{8}{217}\)
b) Ta có: \(A=\dfrac{x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}+\dfrac{1}{\sqrt{x}-2}-\dfrac{\sqrt{x}}{\sqrt{x}+3}\)
\(=\dfrac{x-9+\sqrt{x}+3-\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x+\sqrt{x}-6-x+2\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3\sqrt{x}-6}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3}{\sqrt{x}+3}\)
c) Để \(A>\dfrac{1}{2}\) thì \(A-\dfrac{1}{2}>0\)
\(\Leftrightarrow\dfrac{6-\sqrt{x}-3}{2\left(\sqrt{x}+3\right)}>0\)
\(\Leftrightarrow3-\sqrt{x}>0\)
\(\Leftrightarrow\sqrt{x}< 3\)
hay x<9
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}0\le x< 9\\x\ne4\end{matrix}\right.\)
21 tháng 9 2017
a)\(4\sqrt{x}-5\sqrt{4x}-\sqrt{25x}-3\sqrt{x}-5\)
=\(4\sqrt{x}-10\sqrt{x}-5\sqrt{x}-3\sqrt{x}-5\)
=\(-14\sqrt{x}-5\)
b)\(\sqrt{16x}-5\left(\sqrt{x}-2\right)\sqrt{79x}-5\)
=\(4\sqrt{x}-\left(5\sqrt{x}-10\right)\sqrt{79x}-5\)
=\(4\sqrt{x}-\left(5\sqrt{79}x-10\sqrt{79}x\right)-5\)
=\(4\sqrt{x}+5\sqrt{79}x-5\)