Chứng minh tứ giác ABCD có:
Tổng 2 góc ngoài a1 và c1 bằng tổng 2 góc trọng b và d
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



ta có A+B+C+D=360 độ
Gọi góc ngoài tại đỉnh A là A2
Gọi góc ngoài tại đỉnh B là B2
Ta có:( 180-A2 )+B+(180-C2)+D=360
360-A2+B -C2+D=360
B+D = A2+C2 (dpcm)

(p/s:hình ảnh mang tính chất minh họa)
Gọi \(A_1;C_1\)là góc trong của tứ giác tại đỉnh A và C.
Gọi\(A_2;C_2\)là góc ngoài tại đỉnh A và C
Ta có:
\(\widehat{A_1}+\widehat{A_2}=180^o\)(hai góc kề bù)
\(\Rightarrow\widehat{A_2}=180^o-\widehat{A_1}\)(1)
Ta lại có:
\(\widehat{C_1}+\widehat{C_2}=180^O\)(hai góc kề bù)
\(\Rightarrow\widehat{C_2}=180^o-\widehat{C_1}\)(2)
Từ (1) và (2):
\(\Rightarrow\widehat{A_2}+\widehat{C_2}=180^o-\widehat{A_1}+180^o-\widehat{C_1}\)
\(=360^o-\left(\widehat{A_1}+\widehat{C_1}\right)\)(3)
Tứ giác ABCD có:\(\widehat{A_1}+\widehat{B}+\widehat{C_1}+\widehat{D}=360^o\)(tổng các góc của tứ giác)
\(\Rightarrow\widehat{B}+\widehat{D}=360^o-\left(\widehat{A_1}+\widehat{C_1}\right)\)(4)
Từ (3);(4) suy ra:\(\widehat{A_2}+\widehat{C_2}=\widehat{B}+\widehat{D}\)

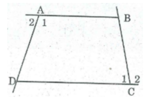
* Gọi ∠ A 1 , ∠ C 1 là góc trong của tứ giác tại đỉnh A và C, ∠ A 2 , ∠ C 2 là góc ngoài tại đỉnh A và C.
Ta có: ∠ A 1 + ∠ A 2 = 180 0 (2 góc kề bù)
⇒ ∠ A 2 = 180 0 - ∠ A 1
∠ C 1 + ∠ C 2 = 180 0 (2 góc kề bù) ⇒ ∠ C 2 = 180 0 - ∠ C 1
Suy ra: ∠ A 2 + ∠ C 2 = 180 0 - ∠ A 1 + 180o - ∠ C 1 = 360 0 – ( ∠ A 1 + ∠ C 1 ) (1)
* Trong tứ giác ABCD ta có:
∠ A 1 + ∠ B + ∠ C 1 + ∠ D = 360 0 (tổng các góc của tứ giác)
⇒ ∠ B + ∠ D = 360 0 - ( ∠ A 1 + ∠ C 1 ) (2)
Từ (1) và (2) suy ra: ∠ A 2 + ∠ C 2 = ∠ B + ∠ D

1 ta có :1 tứ giác có 4 góc và tổng phải bằng 360 độ mà 4 góc nhọn sẽ bé hơn 360(vì 1 góc nhọn <90 độ ) nên cac góc ko thể đều là góc nhọn.Đối với góc tù vẫn tương tự