Đường từ nhà An đến trường dài 1 km dọc theo đường ô tô buýt. Bến xe ngay trước cửa nhà An. An đi với vận tốc 5 km/giờ. Khi An đi học thì một xe cũng rời bến đó và đi cùng chiều với An, vận tốc của xe buýt là 30 km/giờ. Và cứ 4 phút lại có một chuyến xe buýt cùng chiều với An. Hỏi buổi đó có bao nhiêu xe buýt cùng chiều vượt hoặc đuổi kịp An ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 4 2017
Thời gian An đi từ nhà tới trường là:
(1 : 5) x 60 = 12 (phút).
Vì cứ 4 phút có một chuyến xe nên sau khi An đi khỏi nhà 4 phút thì có một xe khác đến cửa nhà An.
Lúc đó An đi cách nhà là:
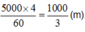
Vận tốc xe buýt hơn vận tốc của An tính theo phút là:
Thời gian ô tô buýt thứ hai đuổi kịp An là:
Ta có: 
Vậy số xe buýt đuổi kịp hoặc vượt An là: 3 (xe).
18 tháng 3 2018
1 giờ 15 phút = 1,25 giờ
Quãng đường bác An đi từ nhà đến bến xe buýt là :
12 * 1.25 = 15 (km)
2 giờ 30 phút = 2,5 giờ
Quãng đường bác An đi từ bến xe buýt đến tỉnh A là :
12 * 2,5 = 30 (km)
Quãng đường bác An đi từ nhà đến tỉnh A là
15 + 30 = 45 (km)
Đáp số : 45 km
30 tháng 3 2018
1 giờ 15 phút = 1,25 giờ
Quãng đường bác An đi từ nhà đến bến xe buýt là :
12 * 1.25 = 15 (km)
2 giờ 30 phút = 2,5 giờ
Quãng đường bác An đi từ bến xe buýt đến tỉnh A là :
12 * 2,5 = 30 (km)
Quãng đường bác An đi từ nhà đến tỉnh A là
15 + 30 = 45 (km)
Đáp số : 45 km
KS
10 tháng 5 2022
đổi` 1 giờ 30 phút = 1,5 giờ`
quãng đường đó là :
` 60 xx 1,5 = 90(km)`
thời gian đi đường của An là :
`90 : 50 = 1,8(giờ) = 1 giờ 48(phút)`
vậy An đén Dồng nai lúc :
`6 giờ 15 phút + 1 giờ 48 phút = 8 giờ 3 phút`
AD
10 tháng 5 2022
1h30p = 1,5h
độ dài của quãng đường đó là: 1,5 x 60 = 90 (km)
thời gian An đi là: 90 : 50 = 1,8 (h) = 1h48p
thời gian An đến nơi là: 6h15p + 1h48p = 8h3p
1 tháng 7 2021
Giải
Gọi x (km/h) là vận tốc đi bộ của An
Gọi y (km/h) là vận tốc đi xe đạp của An
ĐK : 0 < x < y
Vì vận tốc đi xe đạp lớn hơn vận tốc đi bộ là 9km/h nên ta có PT :
\(-x+y=9\) (1)
Thời gian đi buổi sáng là : \(\dfrac{3}{x}\) (h)
Thời gian đi buổi chiều là : \(\dfrac{3}{y}\) (h)
Vì thời gian đi b/c ít hơn thời gian đi b/s là 45' tức \(\dfrac{3}{4}\)h nên ta có PT :
\(\dfrac{3}{x}-\dfrac{3}{y}=\dfrac{3}{4}\) (2)
Từ (1) và (2) ta có HPT :
\(\left\{{}\begin{matrix}-x+y=9\\\dfrac{3}{x}-\dfrac{3}{y}=\dfrac{3}{4}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=y-9\\\dfrac{3}{y-9}-\dfrac{3}{y}=\dfrac{3}{4}\end{matrix}\right.\left(3\right)\)
\(\left(3\right)\Leftrightarrow12y-12\left(y-9\right)=3y\left(y-9\right)\)
\(\Leftrightarrow12y-12y+108=3y^2-27y\)
\(\Leftrightarrow3y^2-27y-108=0\)
\(\Delta=\left(-27\right)^2-4.3.\left(-108\right)=2025\)
\(\Rightarrow\left\{{}\begin{matrix}y_1=\dfrac{27+\sqrt{2025}}{6}=12\left(tm\right)\\y_2=\dfrac{27-\sqrt{2025}}{6}=-3\left(loại\right)\end{matrix}\right.\)
Thế \(y=12\) vào (1) \(\Rightarrow x=3\) (t/m)
Vậy vận tốc đi bộ của An là 3km/h
AH
Akai Haruma
Giáo viên
15 tháng 5 2021
Bài 1: ** Thời gian đi buổi sáng phải nhiều hơn buổi chiều chứ bạn.
Đổi 45 phút thành $\frac{3}{4}$ giờ
Gọi vận tốc đi buổi sáng là $a$ km/h. Khi đó vận tốc buổi chiều là $a+9$ km/h
Thời gian đi buổi sáng: $t_s=\frac{AB}{a}=\frac{3}{a}$ (h)
Thời gian đi buổi chiều: $t_c=\frac{BA}{a+9}=\frac{3}{a+9}$ (h)
Ta có: $t_s-t_c=\frac{3}{a}-\frac{3}{a+9}$
$\Leftrightarrow \frac{3}{4}=\frac{3}{a}-\frac{3}{a+9}$
$\Rightarrow a=3$ (km/h)
Vậy vận tốc đi bộ của An là $3$ km/h
AH
Akai Haruma
Giáo viên
15 tháng 5 2021
Bài 2:
Gọi độ dài chiều dài và chiều rộng HCN lần lượt là $a$ và $b$ (m). ĐK $a>b>0$
Theo bài ra ta có:
\(\left\{\begin{matrix} a+b=28:2=14\\ a^2+b^2=10^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a+b=14\\ (a+b)^2-2ab=100\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} a+b=14\\ ab=48\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=14-b\\ ab=48\end{matrix}\right.\)
\(\Rightarrow (14-b)b=48\)
\(\Leftrightarrow (b-8)(b-6)=0\). Vì $a>b$ mà $a+b=14$ nên $b<7$
Do đó $b=6; a=8$ (m)
giúp mình trả lời bài này nhanh
giúp mình trả lời bài này nhanh