Chứng minh rằng một tứ giác lồi có bốn điểm thuộc các cạnh của tam giác đều cạnh bằng 2016 thì không thể có cả 4 cạnh đều lớn hơn 1008
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn B
Gọi r₁, r₂, r₃, r₄ là khoảng cánh từ điểm M đến bốn mặt của tứ diện.
Gọi S là diện tích một mặt của tứ diện 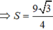
Đường cao của tứ diện là ![]() .
.
Thể tích của tứ diện là 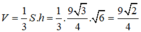 .
.
Mặt khác, ta có:
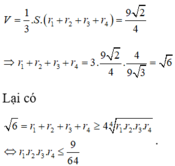

Phát biểu a) là phát biểu sai. Vì một tam giác đều khi có ba cạnh bằng nhau không nhất thiết phải bằng 2cm, có thể bằng 3cm, 4cm, …
Phát biểu b) là đúng. Vì tam giác đều là tam giác có ba cạnh bằng nhau và ba góc bằng nhau.
Phát biểu c) là sai. Vì tam giác IKH chỉ có hai cạnh và hai góc bằng nhau nên chưa đủ điều kiện để tam giác IKH là tam giác đều.

Giả sử số tam giác là k
n=1 => k=1=12
n=2=> k=4=22
n=3=> k=9=32
...
n=2083=> k=20832=4338889
Vậy số tam giác được tạo thành là 4338889 tam giác

Gọi độ dài cạnh của tam giác (đều) ABC là x nên chu vi tam giác ABC là 3x , cạnh và chu vi tứ giác ABCD lần lượt là x - 10 và 4(x - 10).
Theo đề , ta có : 3x = 4(x - 10) = 4x - 40 => 40 = 4x - 3x = x => x - 10 = 40 - 10 = 30.
Vậy độ dài cạnh của tứ giác MNPQ và tam giác ABC lần lượt là 30 cm và 40 cm.
Gọi độ dài cạnh hình tam giác là a
Độ dài cạnh hình tứ giác là b
Theo bài ra ta có: a=10+b
Chu vi hình tam giác là ax3 = (b+10)x3=3xb+30
Chu vi hình tứ giác là bx4
=> 3xb+30=bx4
=> 30 = 4xb-3xb
=> 30 = b
Vậy độ dài cạnh tứ giác MNPQ là 30 cm
=> Độ dài tam giác ABC là 40 cm

Số phần tử của không gian mẫu là số cách chọn 4 đỉnh trong 32 đỉnh để tạo thành tứ giác, Ω = C 32 4
Gọi A là biến cố "chọn được hình chữ nhật".
Để chọn được hình chữ nhật cần chọn 2 trong 16 đường chéo đi qua tâm của đa giác, do đó số phần tử của A là C 16 2
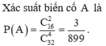
Chọn D

Chọn D.
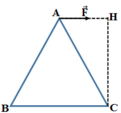
Cánh tay đòn của lực F → là CH. Do đó momen của lực F → đối với trục quay đi qua C và vuông góc với mặt phẳng khung là: MF/C = F.CH = Fℓ 3 /2.