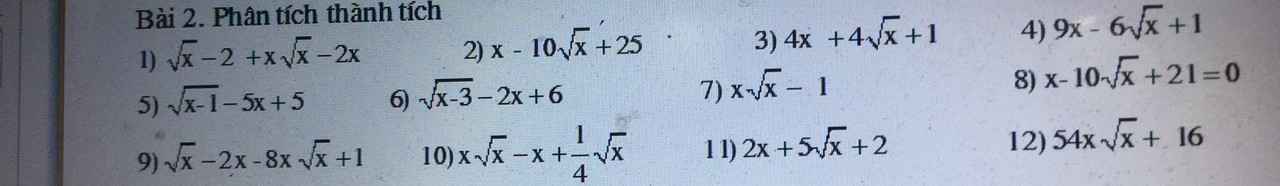các bạn giải hộ mình bài này nha 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NV
0
Những câu hỏi liên quan
9 tháng 10 2016
Cảm ơn bạn nhiều,nhưng bạn có thể giải giúp mình được không?
9 tháng 7 2017
1) Ta có: |x+3| \(\ge\)0; |2x+y-4| \(\ge\)0
\(\Rightarrow\) |x + 3| + |2x + y - 4| \(\ge\) 0
Dấu = xảy ra khi x+3=0 và 2x+y-4 = 0 \(\Rightarrow\)x=-3; y=10
9 tháng 7 2017
1) |x + 3| + |2x + y - 4| = 0
\(\Leftrightarrow\hept{\begin{cases}x+3=0\\2x+y-4=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-3\\-6+y-4=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-3\\y=10\end{cases}}\)
27 tháng 9 2021
4567:567=8(dư 5 )
567:56=10(dư 1)
Mk chưa chắc đúng đâu, k cho mk nhá!
DD
2
1 tháng 1 2022
e: \(=\dfrac{-3}{4}+\dfrac{5}{7}=\dfrac{-21+20}{28}=\dfrac{-1}{28}\)
1 tháng 1 2022
a ) \(\dfrac{6}{13}\) + \(\dfrac{-14}{39}\)
= \(\dfrac{6.3}{13.3}\) + \(\dfrac{-14}{39}\)
= \(\dfrac{18}{39}\) - \(\dfrac{14}{39}\)
= \(\dfrac{4}{39}\)
{ các ý còn lại tương tự }
TK
1
16 tháng 2 2016
- 2x2 + 6x + 5 = 8
- 2x2 + 6x = 3 => 2x[(-x) + 3)] = 3
2x = 1 hoặc (-x) + 3) = 3 => x = 1/2 hoặc x = 0
2x = 3 hoặc (-x) + 3) = 1 => x= 3/2 hoặc x = 2
NK
6
AH
Akai Haruma
Giáo viên
23 tháng 7 2021
1.
\(\sqrt{x}-2+x\sqrt{x}-2x=(\sqrt{x}-2)+(x\sqrt{x}-2x)=(\sqrt{x}-2)+x(\sqrt{x}-2)\)
\(=(\sqrt{x}-2)(1+x)\)
2.
\(x-10\sqrt{x}+25=(\sqrt{x})^2-2.5.\sqrt{x}+5^2=(\sqrt{x}-5)^2\)
3.
\(4x+4\sqrt{x}+1=(2\sqrt{x})^2+2.2\sqrt{x}+1=(2\sqrt{x}+1)^2\)
4.
\(9x-6\sqrt{x}+1=(3\sqrt{x})^2-2.3\sqrt{x}+1=(3\sqrt{x}-1)^2\)
AH
Akai Haruma
Giáo viên
23 tháng 7 2021
5.
\(\sqrt{x-1}-5x+5=\sqrt{x-1}-5(x-1)=\sqrt{x-1}(1-5\sqrt{x-1})\)
6.
\(\sqrt{x-3}-2x+6=\sqrt{x-3}-2(x-3)=\sqrt{x-3}(1-2\sqrt{x-3})\)
7.
\(x\sqrt{x}-1=(\sqrt{x})^3-1^3=(\sqrt{x}-1)(x+\sqrt{x}+1)\)
8.
\(x-10\sqrt{x}+21=x-3\sqrt{x}-(7\sqrt{x}-21)\)
\(=\sqrt{x}(\sqrt{x}-3)-7(\sqrt{x}-3)=(\sqrt{x}-7)(\sqrt{x}-3)\)
9 tháng 8 2015
Gọi UCLN ( n+ 1 ; n+ 2 ) = d ( d : hết cho 1 )
=> n+ 1 chia hết cho d (1)
=> n +2 chia hết cho d (2)
Từ (1) và (2) => n+ 2 - ( n+ 1) chia hết cho d
=> n+ 2 - n - 1 chia hết cho d
=> 1 chia hết cho d
mà 1 lại chia hết cho d
=> d = 1
=> UCLN(n+1;n+2) = 1
=> n+1/n+2 là p/s tối giản