Một xe tải có khối lượng 3 tấn chuyển động qua hai điểm A và B nằm ngang cách nhau 500m biết vận tốc giảm đều từ 30m/s xuống còn 10m/s biết hệ số ma sát giữa xe và mặt đường là 0,2 lấy g= 10 tính a. công của lực ma sát b công của lực kéo của động cơ ô tô
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
18 tháng 6 2017
a. Vì Xe chuyển động thẳng đều nên
F = f m s = μ N = μ m g = 0 , 2.2000.10 = 4000 ( N )
b. v C = 72 ( k m / h ) = 20 ( m / s )
Áp dụng định lý động năng
A = W d C − W d B
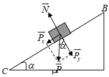
Công của trọng lực
A P = P x . B C = P sin α . B C = m g sin α . B C A P = 2000.10. 1 2 . B C = 10 4 . B C ( J )
⇒ 10 4 . B C = 1 2 . m . v C 2 − 1 2 m . v B 2 ⇒ 10 4 . B C = 1 2 .2000.20 2 − 1 2 .2000.2 2 ⇒ B C = 39 , 6 ( m )
c. Áp dụng định lý động năng
A = W d D − W d C ⇒ A f → m s = 1 2 m v D 2 − 1 2 m v C 2
Công của lực ma sát
A f m s = − f m s . s = − μ N . s = − μ . m g . s / = − μ .2000.10.200 = − μ .4.10 6 ( J )
Dừng lại
v D = 0 ( m / s ) ⇒ − μ 4.10 6 = 0 − 1 2 .2000.20 2 ⇒ μ = 0 , 1
AM
28 tháng 12 2021
Bạn vẽ hình và phân tích lực giúp mình nha.
a. Ta có: \(v=v_0+at\Leftrightarrow8=0+a.20\Leftrightarrow a=0,4\)(m/s2)
Quãng đường xe đi trong 20 giây đầu là: \(x=\dfrac{1}{2}at^2=\dfrac{1}{2}0,4.20^2=80m\)
b.
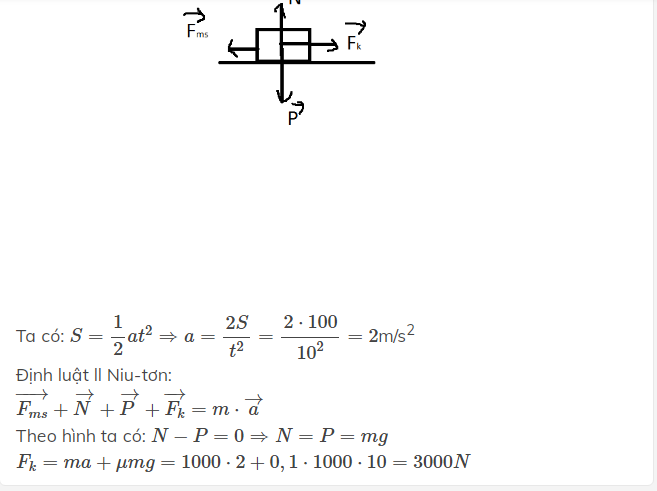
Áp dụng định luật II-Niuton ta có: \(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}+\overrightarrow{F}=m\overrightarrow{a}\)
\(\Rightarrow F=F_{ms}-ma=N\mu-ma=P\mu-ma=5.10^3.10.0,1-5.10^3.0,4=3000N\)
a)Lực ma sát:
\(F_{ms}=\mu\cdot N=\mu mg=0,2\cdot3\cdot1000\cdot10=6000N\)
Công ma sát:
\(A_{ms}=-F_{ms}\cdot s=-6000\cdot500=-3\cdot10^6J\)
b)Bảo toàn động năng:
\(A_{F_k}+A_{F_{ms}}=W_{đ2}-W_{đ1}\)
\(\Rightarrow A_{F_k}-3\cdot10^6=\dfrac{1}{2}\cdot m\left(v_2^2-v_1^2\right)\)
\(\Rightarrow A_{F_k}=\dfrac{1}{2}\cdot3\cdot1000\cdot\left(10^2-30^2\right)+3\cdot10^6=18\cdot10^5J\)