cho tam giác ABC .Gọi D là trung điểm của trung tuyến AM .Tia BD cắt AC tại E.CM:a)AE=1/2 EC b)DE=1/2 BE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CB
Chiến Binh Ngân Nga
25 tháng 5 2016
= Cục cức
Đúng(0)
Những câu hỏi liên quan
2 tháng 7 2015
Bài 1 :
Kẻ dường thẳng x đi qua trung điểm H của ED và BC => cần chứng minh x⊥ED
Lấy điểm I trên x sao cho DI=EI ( I nằm trên nửa mặt chứa A bờ ED )
=>ΔIEH = ΔIDH (= c.c.c)
=>EHI=IHD=180o : 2=90o
=>đpcm
15 tháng 7 2018
1)
Từ M kẻ MK//DE ,MKcắt AC tại K
Xét tg AMK có:
DE//MK
D là tr.điểm AM
=>E là tr.điểm AK
=>AE=EK=1/2AK
Xét tg BEC có:
BE//MK (do DE//MK)
M là tr.điểm BC (AM là tr.tuyến của tg ABC)
=>K là tr.điểm EC
=>KE=1/2EC
Mà AE=EK (cmt)
=>AE=1/2EC (đpcm)
LN
29 tháng 9 2018
Gọi K là trung điểm của BE
Ta có KM là đg trung bình của tam giác BEC
\(KM=\frac{1}{2}EC\)(1)
và KM//AC
Suy ra: góc KMD=DAE(slt)
Chứng minh tam giác ADE=tam giác MDK
Suy ra: \(AE=KM\)(2)
Từ (1) và (2)
Vậy.....
25 tháng 6 2016
bài 1 làm sao vậy sao ko thấy mấy câu trả lời vậy bạn giúp mình giải bài tập số 1 với cảm ơn nhiều
CM
6 tháng 8 2018
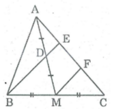
Gọi F là trung điểm của EC.
Trong ∆ CBE, ta có:
M là trung điểm của CB;
F là trung điểm của CE.
Nên MF là đường trung bình của ∆ CBE
⇒ MF// BE (tính chất đường trung bình của tam giác) hay DE// MF
* Trong ∆ AMF, ta có: D là trung điểm của AM
DE // MF
Suy ra: AE = EF (tính chất đường trung bình của tam giác)
Mà EF = FC = EC/2 nên AE = 1/2 EC
AH
Akai Haruma
Giáo viên
13 tháng 10 2021
Lời giải:
Áp dụng định lý Menelaus cho tam giác $AMC$ có $B,D,E$ thẳng hàng:
$\frac{BM}{BC}.\frac{DA}{DM}.\frac{EC}{EA}=1$
$\Leftrightarrow \frac{1}{2}.1.\frac{EC}{EA}=1$
$\Leftrightarrow EC=2EA$ hay $EA=\frac{1}{2}EC$ (đpcm)
