Chứng minh rằng góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



O x y z m m 1 2 3 4
Cho 2 góc xOy và yOz kề bù .
Om ; On lần lượt là tia phân giác của 2 góc đó
\(\Rightarrow\begin{cases}\widehat{O_1}=\widehat{O_2}=\frac{1}{2}.\widehat{xOy}\\\widehat{O_3}=\widehat{O_4}=\frac{1}{2}.\widehat{yOz}\end{cases}\)
\(\Rightarrow\widehat{O_2}+\widehat{O_3}=\frac{1}{2}\left(\widehat{xOy}+\widehat{yOz}\right)=\frac{1}{2}.180^0=90^0\)
=> Đpcm
* Vẽ hình: Vẽ hình hơi xấu chút! ![]()
x y O z t t'
* Viết giả thiết, kết luận:
GT: - Góc xOz và góc yOz là hai góc kề bù
- Ot là tia phân giác của góc xOz
- Ot' là tia phân giác của góc yOz
KL: Góc tot' là 1 góc vuông
* Chứng minh:
Góc xOt = góc tOz = 1/2 . góc xOz (vì Ot là tia phân giác của góc xOz)
Góc yot' = góc t'Oz = 1/2 . góc yOz (vì Ot' là tia phân giác của góc yOz)
Góc xOz + góc yOz = 180 độ (vì 2 góc kề bù)
Vì góc xOz và góc yOz là 2 góc kề bù mà
Ot là tia phân giác xOz
Ot' là tia phân giác yOz
=> Tia Oz nằm giữa hai tia Ot và Ot' nên:
Góc tOt' = góc tOz + góc t'Oz = 1/2 . góc xOz + 1/2 . góc yOz = 1/2 . (góc xOz + góc yOz) = 1/2 . 180 độ = 90 độ
Vậy tOt' là 1 góc vuông.

1,Cho 2 góc xOy và yOz kề bù .
Om ; On lần lượt là tia phân giác của 2 góc đó
⇒{ˆO1=ˆO2=12.ˆxOyˆO3=ˆO4=12.ˆyOz⇒{O1^=O2^=12.xOy^O3^=O4^=12.yOz^
⇒ˆO2+ˆO3=12(ˆxOy+ˆyOz)=12.1800=900⇒O2^+O3^=12(xOy^+yOz^)=12.1800=900
=> Đpcm

* Viết giả thiết, kết luận:
GT: - Góc xOz và góc yOz là hai góc kề bù
- Ot là tia phân giác của góc xOz
- Ot' là tia phân giác của góc yOz
KL: Góc tot' là 1 góc vuông
* Chứng minh:
Góc xOt = góc tOz = 1/2 . góc xOz (vì Ot là tia phân giác của góc xOz)
Góc yot' = góc t'Oz = 1/2 . góc yOz (vì Ot' là tia phân giác của góc yOz)
Góc xOz + góc yOz = 180 độ (vì 2 góc kề bù)
Vì góc xOz và góc yOz là 2 góc kề bù mà
Ot là tia phân giác xOz
Ot' là tia phân giác yOz
=> Tia Oz nằm giữa hai tia Ot và Ot' nên:
Góc tOt' = góc tOz + góc t'Oz = 1/2 . góc xOz + 1/2 . góc yOz = 1/2 . (góc xOz + góc yOz) = 1/2 . 180 độ = 90 độ
Vậy tOt' là 1 góc vuông.
hình tự vẽ nha

A B D E F C
Như hình vẽ trên: DE là pg góc ADB và DF là pg góc ADC
=>ADE = 1/2 (ADB) và ADF = 1/2(ADC)
=>ADE + ADF = EDF = 1/2(ADB + ADC) = 1/2*180 = 90
=>dpcm
Giải:
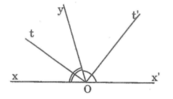
O x' x y t m 0 t' GT xOy và x'Oy kề bù Ot là tia phân giác của góc xOy Ot' là tia phân giác của góc x'Oy KL Ot vuông góc với Ot'
Đặt \(\widehat{xOy}=m^0(0< m^0< 180^0)\)
Hai góc xOy và yOx' là hai góc kề bù nên \(\widehat{xOy}+\widehat{yOx'}=180^0\)do đó \(\widehat{x'Oy}=180^0-\widehat{xOy}=180^0-m^0\)
Theo giả thiết Ot và Ot' lần lượt là tia phân giác của góc xOy và x'Oy nên \(\widehat{tOy}=\frac{1}{2}\widehat{xOy}=\frac{1}{2}m^0\)và \(\widehat{t'Oy}=\frac{1}{2}\widehat{x'Oy}=\frac{1}{2}\left[180^0-m^0\right]\). Tia Oy nằm giữa hai tia Ot và Ot', do đó \(\widehat{tOt}=\widehat{tOy}+\widehat{yOt'}=\frac{1}{2}m^0+\frac{1}{2}\left[180^0-m^0\right]=90^0\)
Vậy \(Ot\perp Ot'\)

Ta có
Hai góc \(\alpha\) và \(\beta\) là 2 góc kề bù => \(\alpha+\beta=180^o\)
=> \(\frac{1}{2}\alpha+\frac{1}{2}\beta=\frac{1}{2}\left(\alpha+\beta\right)\)
mà \(\alpha+\beta\) = 180o
nên \(\frac{1}{2}\alpha+\frac{1}{2}\beta=\frac{1}{2}.180^o=90^o\)
Vậy, góc tạo bởi 2 tia phân giác của 2 góc kề bù là góc vuông

Gọi \(\widehat{xOz}\), \(\widehat{zOy}\) là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của \(\widehat{xOz}\) , \(\widehat{zOy}\)
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy, nên:
\(\hept{\begin{cases}\widehat{uOz}=\widehat{xOu}=\frac{\widehat{xOz}}{2}\\\widehat{zOv}=\widehat{yOv}=\frac{\widehat{zOy}}{2}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}2\widehat{uOz}=\widehat{xOz}\\2\widehat{zOv}=\widehat{zOy}\end{cases}}\)
Ta lại có:
\(\widehat{xOz}+\widehat{zOy}=180^0\) ( kề bù )
\(\Rightarrow2\widehat{uOz}+2\widehat{zOv}=180^0\)
\(\Rightarrow2\left(\widehat{uOz}+\widehat{zOv}\right)=180^0\)
\(\Rightarrow\left(\widehat{uOz}+\widehat{zOv}\right)=180^0\div2\)
\(\Rightarrow\left(\widehat{uOz}+\widehat{zOv}\right)=90^0\)
\(\Rightarrow\widehat{uOv}=90^0\) (vì 2 góc uOz, góc zOv kề nhau)
\(\Rightarrow\) Tia Ou vuông góc tia Ov
Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.
A O E B C D
ta có góc AOE+EOC=180
MÀ BOC=AOB, OED=DOC
vậy BOC+DOE=\(\frac{AOE+EOC}{2}=\frac{180}{2}=90\)

Ta có: ot là tia phân giác của góc xoy => toy = xoy/2
ot' là tia phân giác của góc zoy => t'oy = zoy/2
Suy ra, toy + t'oy = xoy/2 + zoy/2
tot' = (xoy+zoy)/2
Vì xoy và zoy kề bù nên xoy+zoy=180o
=> tot' = 180o/2
tot' = 90o
Vậy ot vuông góc với ot'
TL
Học tốt ^^