Cho hình lăng trụ đều ABC.A'B'C' có tất cả các cạnh bằng a. Tính tan góc giữa đthg AC' và mp(BCC'B')?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
11 tháng 9 2017
Đáp án B
Gọi M, N lần lượt là trung điểm của AC và AM.
Khi đó ΔAHM là tam giác đều và NH ⊥ AC .


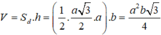
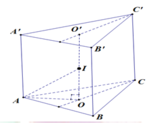



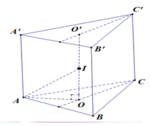

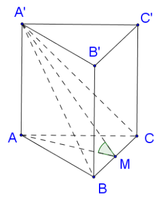




Gọi M là trung điểm BC \(\Rightarrow AM\perp BC\Rightarrow AM\perp\left(BCC'B'\right)\)
\(\Rightarrow\widehat{AC'M}\) là góc giữa AC' và (BCC'B')
\(AM=\dfrac{a\sqrt{3}}{2}\) ; \(C'M=\sqrt{C'C^2+\left(\dfrac{BC}{2}\right)^2}=\dfrac{a\sqrt{5}}{2}\)
\(tan\widehat{AC'M}=\dfrac{AM}{C'M}=\dfrac{\sqrt{15}}{5}\)