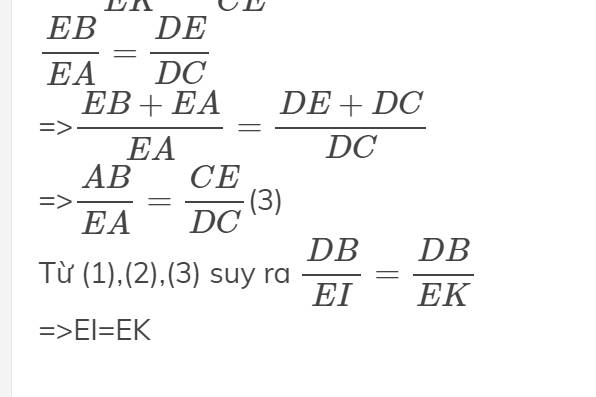Cho tam giác ABC vuông tại A (AB < AC). Kẻ AH vuông góc với BC tại H. Qua B kẻ
đường thẳng vuông góc với AB, cắt đường thẳng AH tại D. Gọi tia AB và tia CD cắt
nhau tại E.
a) Chứng minh: BE/BA = DE/DC
b) Qua E kẻ đường thắng song song với AC, đường thắng này lần lượt cắt các đường
thắng AD, BC tại I, K. Chứng minh: EI = EK;
c) Gọi N là giao điểm của EH và AC; Gọi Q là giao điểm của DN và BC; Gọi P là giao
điểm của BN và AD. Chứng minh: NA = NC và PQ // BD;
d) Gọi G là giao điểm của đường thăng AQ và CD. Qua Q kẻ đường thăng song song
với CE, cắt đường thắng AC tại T. Chứng minh PT vuông góc AD.
mn giúp với ạ, gấp lắm, chỉ cần câu b,c thôi ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có: DB\(\perp\)AB
AC\(\perp\)AB
Do đó: DB//AC
Xét ΔECA có DB//AC
nên \(\dfrac{BE}{BA}=\dfrac{DE}{DC}\)
b: Xét ΔCEK có DB//EK
nên \(\dfrac{DB}{EK}=\dfrac{CD}{CE}\)(1)
Xét ΔAEI có DB//EI
nên \(\dfrac{DB}{EI}=\dfrac{AB}{AE}\left(2\right)\)
Ta có: \(\dfrac{BE}{BA}=\dfrac{DE}{DC}\)
=>\(\dfrac{BE+BA}{BA}=\dfrac{DE+DC}{DC}\)
=>\(\dfrac{AE}{BA}=\dfrac{CE}{DC}\)
=>\(\dfrac{CD}{CE}=\dfrac{AB}{AE}\left(3\right)\)
Từ (1),(2),(3) suy ra EI=EK

a: BD\(\perp\)BA
CA\(\perp\)BA
Do đó: BD//CA
Xét ΔEAC có BD//AC
nên \(\dfrac{EB}{BA}=\dfrac{ED}{DC}\)
b:
AC//BD
BD//IK
Do đó: AC//IK
Xét ΔAEI có BD//EI
nên \(\dfrac{DB}{EI}=\dfrac{AB}{AE}\)(1)
Xét ΔCEK có DB//EK
nên \(\dfrac{DB}{EK}=\dfrac{CD}{CE}\left(2\right)\)
\(\dfrac{EB}{EA}=\dfrac{DE}{DC}\)
=>\(\dfrac{EB+EA}{EA}=\dfrac{DE+DC}{DC}\)
=>\(\dfrac{AB}{EA}=\dfrac{CE}{DC}\)(3)
Từ (1),(2),(3) suy ra \(\dfrac{DB}{EI}=\dfrac{DB}{EK}\)
=>EI=EK