CMR: A là lũy thừa của 2 với A= 4 + 22 + 23+ ......+ 250
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
10 tháng 3 2019
Ta có A = 2A – A = 2( 1 + 2 + 2 2 + 2 3 + . . . + 2 50 ) – ( 1 + 2 + 2 2 + 2 3 + . . . + 2 50 )
= 2 + 4 + 2 3 + 2 4 + . . . + 2 51 – ( 1 + 2 + 2 2 + 2 3 + . . . + 2 50 )
= 6 + 2 3 + 2 4 + . . . + 2 51 – ( 7 + 2 3 + . . . + 2 50 ) = 2 51 - 1
Suy ra : A + 1 = 2 51
Vậy A+1 là một lũy thừa của 2
PT
1
TK
1
T
26 tháng 10 2023
\(A=4+2^2+2^3+...+2^{2006}\)
\(\mathsf{Đặt}:B=2^2+2^3+...+2^{2006}\\2B=2^3+2^4+...+2^{2007}\\2B-B=(2^3+2^4+...+2^{2007})-(2^2+2^3+...+2^{2006})\\B=2^{2007}-2^2\\B=2^{2007}-4\)
Thay \(B=2^{2007}-4\) vào A, ta được:
\(A=4+(2^{2007}-4)\\\Rightarrow A=2^{2007}\)
$\Rightarrow A$ là 1 luỹ thừa của cơ số 2.
Vậy: ...
H9
HT.Phong (9A5)
CTVHS
11 tháng 1
Câu 3:
\(A=3+3^2+...+3^{100}\)
\(3A=3^2+3^3+...+3^{101}\)
\(3A-A=3^2+3^3+...+3^{101}-\left(3+3^2+...+3^{100}\right)\)
\(2A=3^{101}-3\)
Mà: \(2A+3=3^N\)
\(\Rightarrow3^{101}-3+3=3^N\)
\(\Rightarrow3^{101}=3^N\)
\(\Rightarrow N=101\)
Vậy: ...
11 tháng 1
Câu 1:
\(A=4+2^2+...+2^{20}\)
Đặt \(B=2^2+2^3+...+2^{20}\)
=>\(2B=2^3+2^4+...+2^{21}\)
=>\(2B-B=2^3+2^4+...+2^{21}-2^2-2^3-...-2^{20}\)
=>\(B=2^{21}-4\)
=>\(A=B+4=2^{21}-4+4=2^{21}\) là lũy thừa của 2
Câu 6:
Đặt A=1+2+3+...+n
Số số hạng là \(\dfrac{n-1}{1}+1=n-1+1=n\left(số\right)\)
=>\(A=\dfrac{n\left(n+1\right)}{2}\)
=>\(A⋮n+1\)
Câu 5:
\(A=5+5^2+...+5^8\)
\(=\left(5+5^2\right)+\left(5^3+5^4\right)+\left(5^5+5^6\right)+\left(5^7+5^8\right)\)
\(=\left(5+5^2\right)+5^2\left(5+5^2\right)+5^4\left(5+5^2\right)+5^6\left(5+5^2\right)\)
\(=30\left(1+5^2+5^4+5^6\right)⋮30\)
27 tháng 11 2019
Em kiểm tra lại đề bài nhé.
c Câu hỏi của luongngocha - Toán lớp 6 - Học toán với OnlineMath
b. Câu hỏi của son goku - Toán lớp 6 - Học toán với OnlineMath
a. Câu hỏi của Trần Thị Thanh Thảo - Toán lớp 6 - Học toán với OnlineMath
AH
Akai Haruma
Giáo viên
13 tháng 12 2021
Lời giải:
$(2300-22):1+1=2279$
Tổng $A$ là:
$4+\frac{(2300+22).2279}{2}=2645923$. Số này lẻ nên không thể là lũy thừa cơ số 2.
B
2
N
10 tháng 11 2021
Đổi 4 thành 2 mũ 2
Thử xem cs đúng ko . Vì mik chữ thầy toán giả thầy toán hết r
TN
10 tháng 11 2021
Dễ:đổi 4=22
B=22+23+24+...+220
ta có:B=2B-B=(23+24+25+...+221)-(22+23+24+...+220)
= 221-22
Nói trước: đây là mình rút gọn chứ viết mà theo cơ số 2 thì khó quá
GH
2
20 tháng 12 2017
Ta có : A = 4 + 2^2 + 2^3 + 2^4 + ... + 2^20
2A = 8 + 23 + 24 + 25 + ... + 221
suy ra 2A - A = ( 8 + 23 + 24 + 25 + ... + 221 ) - ( 4 + 2^2 + 2^3 + 2^4 + ... + 2^20 )
A = 221 + 8 - 4 - 22 = 221
Vậy A = 221 ( đpcm )
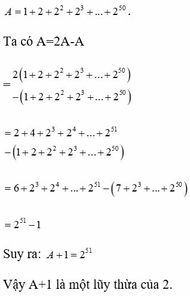
CMR: A là lũy thừa của 2 với A= 4 + 22 + 23+ ......+ 250
GIẢI
2A= 8+ 23+ 24 +........+ 221
2A - A = 8+ 23+24+.......+ 221 - 4 - 22+ 23 +...............+ 220
A= 221 Vậy A là lũy thừa của 2