\(\dfrac{x+1}{2010}+\dfrac{x+2}{2009}+\dfrac{x-3}{2008}+...+\dfrac{x-2009}{2}+\dfrac{x-2010}{1}=-2010\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
OY
1
TA
28 tháng 3 2021
`(x-1)/2013+(x-2)/2012+(x-3)/2011=(x-4)/2010+(x-5)/2009 +(x-6)/2008`
`<=> ((x-1)/2013-1)+((x-2)/2012-1)+((x-3)/2011-1)=( (x-4)/2010-1)+((x-5)/2009-1)+((x-6)/2008-1)`
`<=> (x-2014)/2013 +(x-2014)/2012+(x-2014)/2011=(x-2014)/2010+(x-2014)/2009+(x-2014)/2008`
`<=> x-2014=0` (Vì `1/2013+1/2012+1/2011-1/2010-1/2009-1/2008 \ne 0`)
`<=>x=2014`
Vậy `S={2014}`.
17 tháng 3 2023
\(\dfrac{x-1}{2013}+\dfrac{x-2}{2012}+\dfrac{x-3}{2011}=\dfrac{x-4}{2010}+\dfrac{x-5}{2009}+\dfrac{x-6}{2008}\)
\(\Leftrightarrow\left(\dfrac{x-1}{2013}-1\right)+\left(\dfrac{x-2}{2012}-1\right)+\left(\dfrac{x-3}{2011}-1\right)=\left(\dfrac{x-4}{2010}-1\right)+\left(\dfrac{x-5}{2009}-1\right)+\left(\dfrac{x-6}{2008}-1\right)\)
\(\Leftrightarrow\dfrac{x-2014}{2013}+\dfrac{x-2014}{2012}+\dfrac{x-2014}{2011}=\dfrac{x-2014}{2010}+\dfrac{x-2014}{2009}+\dfrac{x-2014}{2008}\)
\(\Leftrightarrow\dfrac{x-2014}{2013}+\dfrac{x-2014}{2012}+\dfrac{x-2014}{2011}-\dfrac{x-2014}{2010}-\dfrac{x-2014}{2009}-\dfrac{x-2014}{2008}=0\)
\(\Leftrightarrow\left(x-2014\right)\left(\dfrac{1}{2013}+\dfrac{1}{2012}+\dfrac{1}{2011}-\dfrac{1}{2010}-\dfrac{1}{2009}-\dfrac{1}{2008}\right)=0\)
\(\Leftrightarrow\left(x-2014\right).A=0\)
\(\text{Vì A }\ne0\)
\(\Rightarrow x-2014=0\)
\(\Leftrightarrow x=2014\)
\(\text{Vậy phương trình có tập nghiệm là }S=\left\{2014\right\}\)
MD
2
18 tháng 1 2018
\(\dfrac{x-1}{2011}+\dfrac{x-2}{2010}+\dfrac{x-3}{2009}=\dfrac{x-4}{2008}\)
\(\Leftrightarrow\dfrac{x-1}{2011}+\dfrac{x-2}{2012}+\dfrac{x-3}{2009}-\dfrac{x-4}{2008}=0\)
\(\Leftrightarrow\left(\dfrac{x-1}{2011}-1\right)+\left(\dfrac{x-2}{2010}-1\right)+\left(\dfrac{x-3}{2009}-1\right)+\left(\dfrac{x-4}{2008}-1\right)=0\)
\(\Leftrightarrow\dfrac{x-2012}{2011}+\dfrac{x-2012}{2010}+\dfrac{x-2012}{2009}-\dfrac{x-2012}{2008}=0\)
\(\Leftrightarrow\left(x-2012\right)\left(\dfrac{1}{2011}+\dfrac{1}{2010}+\dfrac{1}{2009}-\dfrac{1}{2008}\right)=0\)
Mà \(\dfrac{1}{2011}+\dfrac{1}{2010}+\dfrac{1}{2009}-\dfrac{1}{2008}\ne0\)
\(\Leftrightarrow x-2012=0\Leftrightarrow x=2012\)
Vậy ...
S
18 tháng 1 2018
\(\dfrac{x-1}{2011}+\dfrac{x-2}{2010}+\dfrac{x-3}{2009}=\dfrac{x-4}{2008}\)
=> \(\dfrac{x-1}{2011}-1+\dfrac{x-2}{2010}-1+\dfrac{x-3}{2009}-1=\dfrac{x-4}{2008}-1-2\)
=>\(\dfrac{x-2012}{2011}+\dfrac{x-2012}{2010}+\dfrac{x-2012}{2009}=\dfrac{x-2012}{2008}-\dfrac{x-2012}{\left(x-2012\right):2}\)
=> \(\dfrac{x-2012}{2011}+\dfrac{x-2012}{2010}+\dfrac{x-2012}{2009}-\dfrac{x-2012}{2008}-\dfrac{x-2012}{\left(x-2012\right):2}=0\)=> x - 2012 ( \(\dfrac{1}{2011}+\dfrac{1}{2010}+\dfrac{1}{2009}-\dfrac{1}{2008}-\dfrac{1}{\left(x-2012\right):2}\)) = 0
Vì \(\dfrac{1}{2011}+\dfrac{1}{2010}+\dfrac{1}{2009}-\dfrac{1}{2008}-\dfrac{1}{\left(x-2012\right):2}\) \(\ge\) 0
=> x - 2012 = 0
=> x = 2012
PT
1
25 tháng 7 2017
\(\dfrac{x+1}{2011}+\dfrac{x+2}{2010}+\dfrac{x+3}{2009}+\dfrac{x+4}{2008}=-4\)
\(\Rightarrow\dfrac{x+1}{2011}+1+\dfrac{x+2}{2010}+1+\dfrac{x+3}{2009}+1+\dfrac{x+4}{2008}+1=0\)
\(\Rightarrow\dfrac{x+2012}{2011}+\dfrac{x+2012}{2010}+\dfrac{x+2012}{2009}+\dfrac{x+2012}{2008}=0\)
\(\Rightarrow\left(x+2012\right)\left(\dfrac{1}{2011}+\dfrac{1}{2010}+\dfrac{1}{2009}+\dfrac{1}{2008}\right)=0\)
Mà \(\dfrac{1}{2011}+\dfrac{1}{2010}+\dfrac{1}{2009}+\dfrac{1}{2008}\ne0\)
\(\Rightarrow x+2012=0\Rightarrow x=-2012\)
Vậy x = -2012
NL
3
H
28 tháng 8 2017
Giải:
\(\dfrac{x+4}{2008}+\dfrac{x+3}{2009}=\dfrac{x+2}{2010}+\dfrac{x+1}{2011}\)
\(\Leftrightarrow\dfrac{x+4}{2008}+\dfrac{x+3}{2009}+2=\dfrac{x+2}{2010}+\dfrac{x+1}{2011}+2\)
\(\Leftrightarrow\dfrac{x+4}{2008}+1+\dfrac{x+3}{2009}+1=\dfrac{x+2}{2010}+1+\dfrac{x+1}{2011}+1\)
\(\Leftrightarrow\dfrac{x+4+2008}{2008}+\dfrac{x+3+2009}{2009}=\dfrac{x+2+2010}{2010}+\dfrac{x+1+2011}{2011}\)
\(\Leftrightarrow\dfrac{x+2012}{2008}+\dfrac{x+2012}{2009}=\dfrac{x+2012}{2010}+\dfrac{x+2012}{2011}\)
\(\Leftrightarrow\dfrac{x+2012}{2008}+\dfrac{x+2012}{2009}-\dfrac{x+2012}{2010}-\dfrac{x+2012}{2011}=0\)
\(\Leftrightarrow\left(x+2012\right)\left(\dfrac{1}{2008}+\dfrac{1}{2009}-\dfrac{1}{2010}-\dfrac{1}{2011}\right)=0\)
Vì \(\dfrac{1}{2008}+\dfrac{1}{2009}-\dfrac{1}{2010}-\dfrac{1}{2011}\ne0\)
Nên \(x+2012=0\)
\(\Leftrightarrow x=0-2012\)
\(\Leftrightarrow x=-2012\)
Vậy \(x=-2012\).
Chúc bạn học tốt!
28 tháng 8 2017
\(\dfrac{x+4}{2008}+\dfrac{x+3}{2009}=\dfrac{x+2}{2010}+\dfrac{x+1}{2011}\)
\(\Rightarrow\dfrac{x+4}{2008}+1+\dfrac{x+3}{2009}+1=\dfrac{x+2}{2010}+1+\dfrac{x+1}{2011}+1\)
\(\Rightarrow\dfrac{x+2012}{2008}+\dfrac{x+2012}{2009}=\dfrac{x+2012}{2010}+\dfrac{x+2012}{2011}\)
\(\Rightarrow\dfrac{x+2012}{2008}+\dfrac{x+2012}{2009}-\dfrac{x+2012}{2010}-\dfrac{x+2012}{2011}=0\)
\(\Rightarrow\left(x+2012\right)\left(\dfrac{1}{2008}+\dfrac{1}{2009}-\dfrac{1}{2010}-\dfrac{1}{2011}\right)=0\)
Vì \(\dfrac{1}{2008}+\dfrac{1}{2009}-\dfrac{1}{2010}-\dfrac{1}{2011}\ne0\)
Nên:
\(x+2012=0\Rightarrow x=-2012\)
11 tháng 3 2018
đkxđ với mọi x
đặt a=x2+x+1
\(\dfrac{a}{a+1}+\dfrac{a+1}{a+2}=\dfrac{7}{6}\)
<=> \(\dfrac{6a\left(a+2\right)}{6\left(a+1\right)\left(a+2\right)}+\dfrac{6\left(a+1\right)^2}{6\left(a+1\right)\left(a+2\right)}=\dfrac{7\left(a+1\right)\left(a+2\right)}{6\left(a+1\right)\left(a+2\right)}\)
=> 6a(a+2) +6(a+1)2 =7(a+1)(a+2)
<=> 6a2+12a +6a2 +12a+6 =a2 +21a+14
<=> 12a2 -a2+24a-21a+6-14=0
<=> 11a2+3a-8=0
<=> 11a2 +11a-8a-8=0
<=> (11a2 +11a)-(8a+8)=0
<=> 11a(a+1)-8(a+1)=0
<=> (a+1)(11a-8)=0
=> a=-1 và a=\(\dfrac{8}{11}\)
thay a=x2+x+1 ta đc
x2+x+1=-1
<=> x2+x+2 =0 (vô nghiệm)
và x2+x+\(\dfrac{3}{11}\) =0(vô nghiệm )
vậy pt trên vô nghiệm
12 tháng 3 2018
c) \(8\left(x+\dfrac{1}{x}\right)^2+4\left(x^2+\dfrac{1}{x^2}\right)^2-4\left(x^2+\dfrac{1}{x^2}\right)\left(x+\dfrac{1}{x}\right)^2=\left(x+4\right)^2\left(2\right)\)ĐKXĐ : x # 0
( 2) <=> \(8\left(x+\dfrac{1}{x}\right)^2+4\left(x^2+\dfrac{1}{x^2}\right)\left[\left(x^2+\dfrac{1}{x^2}\right)-\left(x+\dfrac{1}{x}\right)^2\right]=\left(x+4\right)^2\)
\(< =>8\left(x+\dfrac{1}{x}\right)^2+4\left(x^2+\dfrac{1}{x^2}\right).\left(-2\right)=\left(x+4\right)^2\)
\(< =>8.\left[\left(x+\dfrac{1}{x}\right)^2-x^2-\dfrac{1}{x^2}\right]=\left(x+4\right)^2\)
\(< =>16=\left(x+4\right)^2\)
<=> x2 + 8x = 0
<=> x( x + 8) = 0
<=> x = 0 ( KTM ) hoặc x = - 8 ( TM )
Vậy,....
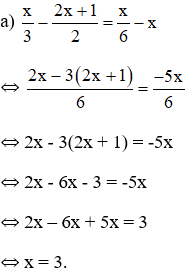
\(\Leftrightarrow\dfrac{x+1}{2010}+1+\dfrac{x+2}{2009}+1+...+\dfrac{x+2009}{2}+1+\dfrac{x+2010}{1}+1=0\)
=>x+2011=0
hay x=-2011