cho tam giác ABC có M nằm trong tam giác ABC chứng minh rằng MC+MC<AB+BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 3 2019
Trong ΔAMB, ta có:
MA + MB > AB (bất đẳng thức tam giác) (1)
Trong ΔAMC, ta có:
MA + MC > AC (bất đẳng thức tam giác) (2)
Trong ΔBMC, ta có:
MB + MC > BC (bất đẳng thức tam giác) (3)
Cộng từng vế (1), (2) và (3), ta có:
MA + MB + MA + MC + MB + MC > AB + AC + BC
⇔ 2(MA + MB + MC) > AB + AC + BC
Vậy MA + MB + MC > (AB + AC + BC) / 2
TP
20 tháng 7 2017
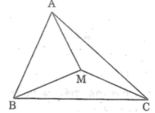
A M B C Hình 45 (h.45) Xét \(\Delta ABM:\)MA+MB>AB (1)
Xét \(\Delta AMC:\) MA+MC>AC (2)
Xét \(\Delta BMC:\) MB+MC>BC (3)
Cộng từng vế (1), (2), (3):
2(MA+MB+MC)>\(\text{AB+AC+BC}\)
Suy ra :
MA+MB+MC>\(\dfrac{\text{AB+AC+BC}}{2}\)
MA
1
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 2 2022
Kéo dài AM cắt BC tại D \(\Rightarrow\) D nằm giữa B và C
Áp dụng BĐT tam giác ABD:
\(AB+BD>AD\Rightarrow AB+BD>AM+MD\)
Áp dụng BĐT tam giác MCD:
\(MD>MC-CD\)
\(\Rightarrow AB+BD+MD>AM+MD+MC-CD\)
\(\Rightarrow AB+BD+CD>AM+MC\)
\(\Rightarrow AB+BC>AM+MC\)
LT
1
`Answer:`
Mình đã sửa lại đề nhé.
Kẻ BM cắt AC ở D
Xét `\triangleABD:`
`BD<AB+AD<=>MB+MD<AB+AD(1)`
Xét `\triangleMDC:`
`MC<MD+DC(2)`
Từ `(1)` và `(2)=>MB+MC+MD<AB+AD+DC+MD=>MB+MC>AB+AC`
Chứng minh tương tự, có `MA+MC<AB+BC;MA+MB<AC+BC`
Do vậy `2(MA+MC)<2(AB+BC)<=>MA+MC<AB+BC`