Mn giúp em câu 2 và câu 3 với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KT
1
14 tháng 1
1: \(\dfrac{11}{x^4y};\dfrac{3}{xy^3}\)
\(\dfrac{11}{x^4y}=\dfrac{11\cdot y^2}{x^4y^3}=\dfrac{11y^2}{x^4y^3}\)
\(\dfrac{3}{xy^3}=\dfrac{3\cdot x^3}{xy^3\cdot x^3}=\dfrac{3x^3}{x^4y^3}\)
2: \(\dfrac{2}{3x^3y^2};\dfrac{3}{4x^7y}\)
\(\dfrac{2}{3x^3y^2}=\dfrac{2\cdot4\cdot x^4}{3x^3y^2\cdot4x^4}=\dfrac{8x^4}{12x^7y^2}\)
\(\dfrac{3}{4x^7y}=\dfrac{3\cdot3\cdot y}{4x^7y\cdot3y}=\dfrac{9y}{12x^7y^2}\)
C
21 tháng 12 2022
\(x+\dfrac{3}{5}=\left(-\dfrac{2}{5}\right)^2\\ x+\dfrac{3}{5}=\dfrac{4}{25}\\ x=\dfrac{4}{25}-\dfrac{3}{5}\\ x=\dfrac{4}{25}-\dfrac{15}{25}\\ x=-\dfrac{11}{25}\)
__
\(\left|x+\dfrac{3}{4}\right|-\dfrac{5}{6}=0\\ \left|x+\dfrac{3}{4}\right|=0+\dfrac{5}{6}\\ \left|x+\dfrac{3}{4}\right|=\dfrac{5}{6}\\ \left|x+\dfrac{3}{4}\right|=\pm\dfrac{5}{6}\\ \left[{}\begin{matrix}x+\dfrac{3}{4}=\dfrac{5}{6}\\x+\dfrac{3}{4}=-\dfrac{5}{6}\end{matrix}\right.\\ \left[{}\begin{matrix}x=\dfrac{5}{6}-\dfrac{3}{4}\\x=-\dfrac{5}{6}-\dfrac{3}{4}\end{matrix}\right.\\ \left[{}\begin{matrix}x=\dfrac{20}{24}-\dfrac{18}{24}\\x=-\dfrac{20}{24}-\dfrac{18}{24}\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=\dfrac{2}{24}\\x=-\dfrac{38}{24}\end{matrix}\right.\\ \left[{}\begin{matrix}x=\dfrac{1}{12}\\x=-\dfrac{19}{12}\end{matrix}\right.\)
__
\(\left(x+\dfrac{3}{7}\right)^2=\dfrac{25}{49}\\ \left(x+\dfrac{3}{7}\right)^2=\left(\pm\dfrac{5}{7}\right)^2\\ \left[{}\begin{matrix}x+\dfrac{3}{7}=\dfrac{5}{7}\\x+\dfrac{3}{7}=-\dfrac{5}{7}\end{matrix}\right.\\ \left[{}\begin{matrix}x=\dfrac{5}{7}-\dfrac{3}{7}\\x=-\dfrac{5}{7}-\dfrac{3}{7}\end{matrix}\right.\\ \left[{}\begin{matrix}x=\dfrac{2}{7}\\x=-\dfrac{8}{7}\end{matrix}\right.\)
22 tháng 12 2022
Câu 2:
a: x=4/25-3/5=4/25-15/25=-11/25
b: =>|x+3/4|=5/6
=>x+3/4=5/6 hoặc x+3/4=-5/6
=>x=5/6-3/4=10/12-9/12=1/12 hoặc x=-10/12-9/12=-19/12
c: =>x+3/7=5/7 hoặc x+3/7=-5/7
=>x=-8/7 hoặc x=2/7
mn giúp em 2 câu 3 với ạ,em cảm ơn
S
8 tháng 11 2023
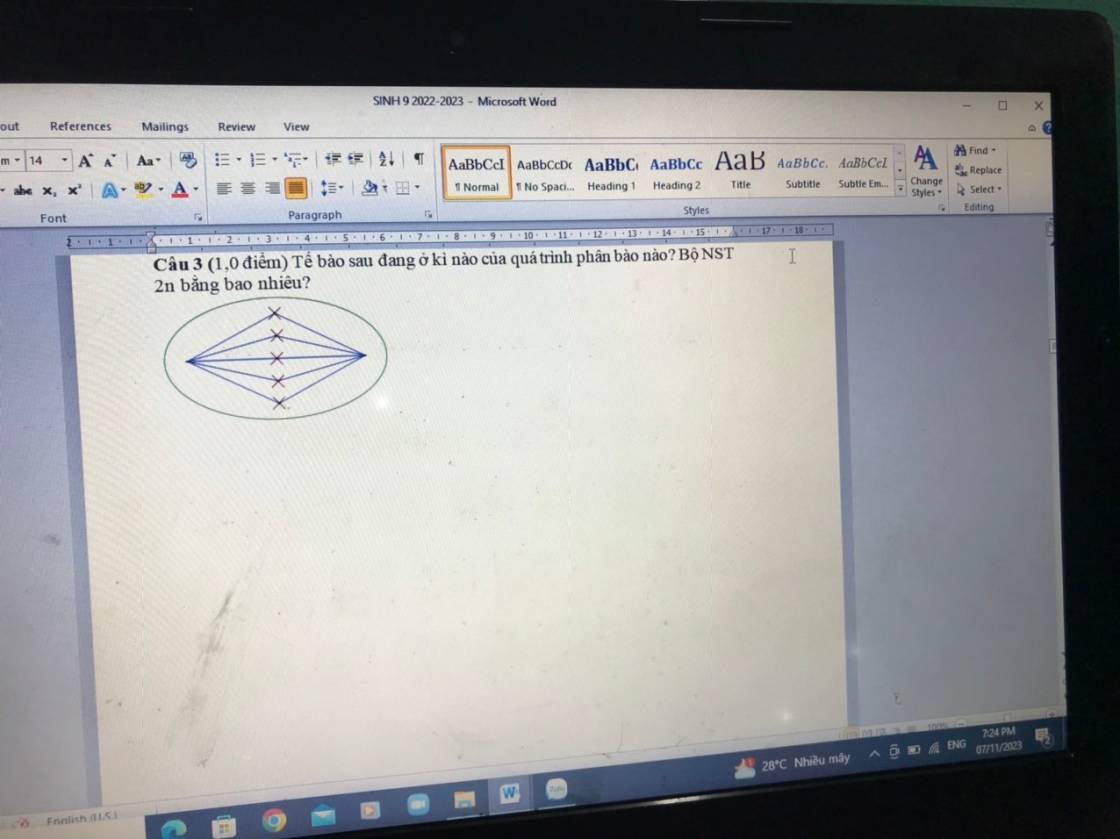
Câu 3 (trên) : Tế bào đang ở kì giữa II của giảm phân
Giải thích : Do số NST trên hình lẻ nên bộ NST là n chứ không phải là 2n vì 2n luôn chẵn -> chỉ có ở giảm phân tạo giao tử, mà các NST xếp thành 1 hàng trên mp xích đạo nên đây là kì giữa II
Bộ NST 2n = 5.2 = 10
Câu 3 (dưới) : Tế bào đang ở kì sau nguyên phân hoặc giảm phân II
Giải thích : Vì ta thấy có 8 NST là số chẵn, mà các NST phân ly về 2 cực tế bào nên đây là Kì sau, do số NST là số chẵn, NST ở dạng đơn nên đây là kỳ sau nguyên phân (4n đơn) hoặc giảm phân II (2n đơn)
Bộ NST : \(\left[{}\begin{matrix}2n=4\\2n=8\end{matrix}\right.\)
DT
3
2 tháng 8 2021
8) \(\dfrac{x+7}{3}+\dfrac{x+5}{4}=\dfrac{x+3}{5}+\dfrac{x+1}{6}\)
\(\Rightarrow\dfrac{x+7}{3}+\dfrac{x+5}{4}-\dfrac{x+3}{5}-\dfrac{x+1}{6}=0\)
\(\Rightarrow\dfrac{x+7}{3}+2+\dfrac{x+5}{4}+2-\dfrac{x+3}{5}-2-\dfrac{x+1}{6}-2=0+2+2-2-2\)
\(\Rightarrow\left(\dfrac{x+7}{3}+2\right)+\left(\dfrac{x+5}{4}+2\right)-\left(\dfrac{x+3}{5}+2\right)-\left(\dfrac{x+1}{6}+2\right)=0\)
\(\Rightarrow\left(\dfrac{x+7}{3}+\dfrac{6}{3}\right)+\left(\dfrac{x+5}{4}+\dfrac{8}{4}\right)-\left(\dfrac{x+3}{5}+\dfrac{10}{5}\right)-\left(\dfrac{x+1}{6}+\dfrac{12}{2}\right)=0\)
\(\Rightarrow\left(x+13\right)\left(\dfrac{1}{3}+\dfrac{1}{4}-\dfrac{1}{5}-\dfrac{1}{6}\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+13=0\\\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}=0\end{matrix}\right.\)
\(x+13=0\)
\(\Rightarrow x=-13\)
\(\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}=0\)
\(\dfrac{13}{60}=0\) (vô lí)
Vậy \(x=-13\)
9) Bạn chuyển vế rồi cộng 3 vào từng mỗi số
BD
1
22 tháng 7 2021
Câu 2:
Ta có: \(x^2-2\left(m+1\right)x+m^2+4=0\)
a=1; b=-2m-2; \(c=m^2+4\)
\(\text{Δ}=b^2-4ac\)
\(=\left(-2m-2\right)^2-4\cdot\left(m^2+4\right)\)
\(=4m^2+8m+4-4m^2-16\)
=8m-12
Để phương trình có hai nghiệm phân biệt thì Δ>0
\(\Leftrightarrow8m>12\)
hay \(m>\dfrac{3}{2}\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)=2m+2\\x_1x_2=m^2+4\end{matrix}\right.\)
Vì x1 là nghiệm của phương trình nên ta có:
\(x_1^2-2\left(m+1\right)\cdot x_1+m^2+4=0\)
\(\Leftrightarrow x_1^2=2\left(m+1\right)x_1-m^2-4\)
Ta có: \(x_1^2+2\left(m+1\right)x_2=2m^2+20\)
\(\Leftrightarrow2\left(m+1\right)x_1-m^2-4+2\left(m+1\right)x_2-2m^2-20=0\)
\(\Leftrightarrow2\left(m+1\right)\left(x_1+x_2\right)-3m^2-24=0\)
\(\Leftrightarrow2\left(m+1\right)\cdot\left(2m+2\right)-3m^2-24=0\)
\(\Leftrightarrow4m^2+8m+4-3m^2-24=0\)
\(\Leftrightarrow m^2+8m-20=0\)
Đến đây bạn tự tìm m là xong rồi
TN
Mn giúp em bài 3 câu bc với em tính số xấu quá, mong mn giúp ạ:(
1
5 tháng 8 2021
Bài 3:
2) Ta có: \(B=2x\left(y-z\right)+\left(z-y\right)\left(x+t\right)\)
\(=2x\left(y-z\right)-\left(x+t\right)\left(y-z\right)\)
\(=\left(y-z\right)\left(x-t\right)\)
\(=\left(24-10,6\right)\left(18,3+31,7\right)\)
\(=13,4\cdot50=670\)
3) Ta có: \(C=\left(x-y\right)\left(y+z\right)+y\left(y-x\right)\)
\(=\left(x-y\right)\left(y+z\right)-y\left(x-y\right)\)
\(=z\left(x-y\right)\)
\(=1.5\left(0.86-0.26\right)\)
\(=0,9\)
H
31 tháng 12 2022
$C + O_2 \xrightarrow{t^o} CO_2$
$2C + O_2 \xrightarrow{t^o} 2CO$
Gọi $n_{CO_2} = a(mol) ; n_{CO} =b (mol)$
Ta có: $M_B = \dfrac{44a + 28b}{a + b} = 15.2 = 30(1)$
Theo PTHH : $n_{O_2} = a + 0,5b = \dfrac{2,88}{32} = 0,09(2)$
Từ (1)(2) suy ra : a = 0,02 ; b = 0,14
$\%V_{CO_2} = \dfrac{0,02}{0,02 + 0,14}.100\% = 12,5\%$
$\%V_{CO} = 100\% - 12,5\% = 87,5\%$
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
25 tháng 7 2021
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HM là đường cao ứng với cạnh huyền AB, ta được:
\(AM\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HN là đường cao ứng với cạnh huyền AC, ta được:
\(AN\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
9 tháng 12 2021
Tham khảo:
Cố gắng học tập, rèn luyện để trở thành một công dân tốt trong xã hộiGiữ gìn và bảo vệ những truyền thống văn hóa tốt đẹp của quê hương, đất nước.Vệ sinh khu phố mình đang ở cũng như xung quanh, hạn chế thả rác bừa bãiTuyên truyền việc tốt để các bạn nhỏ và mọi người thể hiện tình yêu quê hương đất nước,...9 tháng 12 2021
cô em nói không đc chép mạng ạ, có 1 bn kia chép cô giận quá nên cho 0đ
mn giúp em vs ạ !