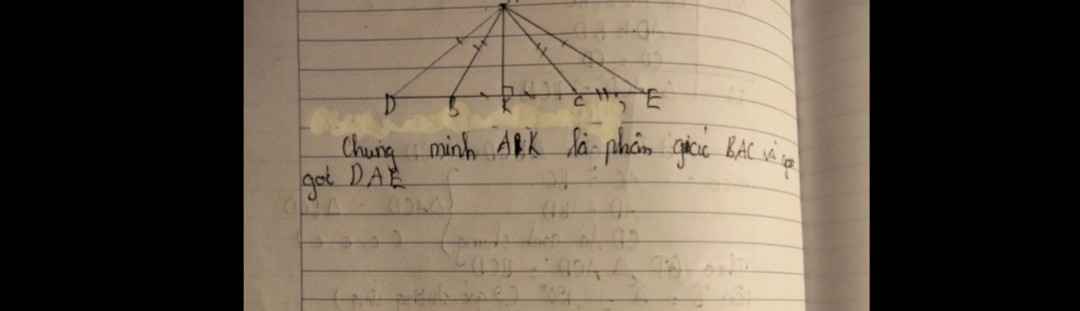
Ai giải hộ mình bài 5;6;11;12 với mình cần gấp hôm nay
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TN
0
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
19 tháng 7 2021
Lần sau bạn chú ý viết đầy đủ đề.
1.
\(\sqrt{9+4\sqrt{5}-\sqrt{9-4\sqrt{5}}}=\sqrt{9+4\sqrt{5}-\sqrt{5-2\sqrt{4.5}+4}}\)
\(=\sqrt{9+4\sqrt{5}-\sqrt{(\sqrt{5}-\sqrt{4})^2}}=\sqrt{9+4\sqrt{5}-(\sqrt{5}-\sqrt{4})}\)
\(=\sqrt{9+4\sqrt{5}-\sqrt{5}+2}=\sqrt{11+3\sqrt{5}}\)
AH
Akai Haruma
Giáo viên
19 tháng 7 2021
2.
\(\sqrt{8-2\sqrt{7}-\sqrt{8+2\sqrt{7}}}=\sqrt{8-2\sqrt{7}-\sqrt{7+2\sqrt{7}+1}}\)
\(=\sqrt{8-2\sqrt{7}-\sqrt{(\sqrt{7}+1)^2}}\)
\(=\sqrt{8-2\sqrt{7}-\sqrt{7}-1}=\sqrt{7-3\sqrt{7}}\)
5 tháng 8 2021
22,
1, Đặt √(3-√5) = A
=> √2A=√(6-2√5)
=> √2A=√(5-2√5+1)
=> √2A=|√5 -1|
=> A=\(\dfrac{\sqrt{5}-1}{\text{√2}}\)
=> A= \(\dfrac{\sqrt{10}-\sqrt{2}}{2}\)
2, Đặt √(7+3√5) = B
=> √2B=√(14+6√5)
=> √2B=√(9+2√45+5)
=> √2B=|3+√5|
=> B= \(\dfrac{3+\sqrt{5}}{\sqrt{2}}\)
=> B= \(\dfrac{3\sqrt{2}+\sqrt{10}}{2}\)
3,
Đặt √(9+√17) - √(9-√17) -\(\sqrt{2}\)=C
=> √2C=√(18+2√17) - √(18-2√17) -\(2\)
=> √2C=√(17+2√17+1) - √(17-2√17+1) -\(2\)
=> √2C=√17+1- √17+1 -\(2\)
=> √2C=0
=> C=0
26,
|3-2x|=2\(\sqrt{5}\)
TH1: 3-2x ≥ 0 ⇔ x≤\(\dfrac{-3}{2}\)
3-2x=2\(\sqrt{5}\)
-2x=2\(\sqrt{5}\) -3
x=\(\dfrac{3-2\sqrt{5}}{2}\) (KTMĐK)
TH2: 3-2x < 0 ⇔ x>\(\dfrac{-3}{2}\)
3-2x=-2\(\sqrt{5}\)
-2x=-2√5 -3
x=\(\dfrac{3+2\sqrt{5}}{2}\) (TMĐK)
Vậy x=\(\dfrac{3+2\sqrt{5}}{2}\)
6 tháng 8 2021
2, \(\sqrt{x^2}\)=12 ⇔ |x|=12 ⇔ x=12, -12
3, \(\sqrt{x^2-2x+1}\)=7
⇔ |x-1|=7
TH1: x-1≥0 ⇔ x≥1
x-1=7 ⇔ x=8 (TMĐK)
TH2: x-1<0 ⇔ x<1
x-1=-7 ⇔ x=-6 (TMĐK)
Vậy x=8, -6
4, \(\sqrt{\left(x-1\right)^2}\)=x+3
⇔ |x-1|=x+3
TH1: x-1≥0 ⇔ x≥1
x-1=x+3 ⇔ 0x=4 (KTM)
TH2: x-1<0 ⇔ x<1
x-1=-x-3 ⇔ 2x=-2 ⇔x=-1 (TMĐK)
Vậy x=-1
AT
12 tháng 7 2021
\(\sqrt{13+\sqrt{48}}=\sqrt{13+\sqrt{4.12}}=\sqrt{13+2\sqrt{12}}=\sqrt{\left(\sqrt{12}+1\right)^2}\)
\(=\sqrt{12}+1=2\sqrt{3}+1\)
\(\Rightarrow\sqrt{5-\sqrt{13+\sqrt{48}}}=\sqrt{5-2\sqrt{3}-1}=\sqrt{4-2\sqrt{3}}=\sqrt{\left(\sqrt{3}-1\right)^2}\)
\(=\sqrt{3}-1\)
\(\Rightarrow\sqrt{3+\sqrt{5-\sqrt{13+\sqrt{48}}}}=\sqrt{3+\sqrt{3}-1}=\sqrt{2+\sqrt{3}}\)
\(\Rightarrow\sqrt{\dfrac{4+2\sqrt{3}}{2}}=\sqrt{\dfrac{\left(\sqrt{3}+1\right)^2}{2}}=\dfrac{\sqrt{3}+1}{\sqrt{2}}\)
\(\Rightarrow2\sqrt{3+\sqrt{5-\sqrt{13+\sqrt{48}}}}==2.\dfrac{\sqrt{3}+1}{\sqrt{2}}=\sqrt{6}+\sqrt{2}\)
2) biến đổi khúc sau như câu 1:
\(\Rightarrow\sqrt{6+2\sqrt{5-\sqrt{13+\sqrt{48}}}}=\sqrt{6+2\left(\sqrt{3}-1\right)}=\sqrt{4+2\sqrt{3}}\)
\(=\sqrt{\left(\sqrt{3}+1\right)^2}=\sqrt{3}+1\)
AT
12 tháng 7 2021
1) Ta có: \(\sqrt{5-\sqrt{13+\sqrt{48}}}=\sqrt{5-\sqrt{13+\sqrt{4.12}}}=\sqrt{5-\sqrt{13+2\sqrt{12}}}\)
\(=\sqrt{5-\sqrt{\left(\sqrt{12}\right)^2+2.\sqrt{12}+1^2}}=\sqrt{5-\sqrt{\left(\sqrt{12}+1\right)^2}}=\sqrt{5-\left|\sqrt{4.3}+1\right|}\)
\(=\sqrt{5-\left(2\sqrt{3}+1\right)}=\sqrt{5-2\sqrt{3}-1}=\sqrt{4-2\sqrt{3}}\)
\(=\sqrt{\left(\sqrt{3}\right)^2-2.\sqrt{3}.1+1^2}=\sqrt{\left(\sqrt{3}-1\right)^2}=\left|\sqrt{3}-1\right|=\sqrt{3}-1\)
\(\Rightarrow2\sqrt{3+\sqrt{5-\sqrt{13+\sqrt{48}}}}=2\sqrt{3+\sqrt{3}-1}=2\sqrt{2+\sqrt{3}}\)
\(=2\sqrt{\dfrac{4+2\sqrt{3}}{2}}=2\sqrt{\dfrac{\left(\sqrt{3}\right)^2+2.\sqrt{3}.1+1^2}{2}}=2\sqrt{\dfrac{\left(\sqrt{3}+1\right)^2}{2}}\)
\(=2.\dfrac{\left|\sqrt{3}+1\right|}{\sqrt{2}}=\sqrt{2}\left(\sqrt{3}+1\right)=\sqrt{6}+\sqrt{2}\)
2) Ta có: \(\sqrt{5-\sqrt{13+\sqrt{48}}}=\sqrt{3}-1\) (như trên)
\(\Rightarrow\sqrt{6+2\sqrt{5-\sqrt{13+\sqrt{48}}}}=\sqrt{6+2\left(\sqrt{3}-1\right)}=\sqrt{4+2\sqrt{3}}\)
\(=\sqrt{\left(\sqrt{3}\right)^2+2.\sqrt{3}.1+1^2}=\sqrt{\left(\sqrt{3}+1\right)^2}=\left|\sqrt{3}+1\right|=\sqrt{3}+1\)
AH
Akai Haruma
Giáo viên
19 tháng 7 2021
Bài 1:
a.
\(\frac{1}{2\sqrt{2}-3\sqrt{3}}=\frac{2\sqrt{2}+3\sqrt{3}}{(2\sqrt{2}-3\sqrt{3})(2\sqrt{2}+3\sqrt{3})}=\frac{2\sqrt{2}+3\sqrt{3}}{(2\sqrt{2})^2-(3\sqrt{3})^2}=\frac{2\sqrt{2}+3\sqrt{3}}{-19}\)
b.
\(=\sqrt{\frac{(3-\sqrt{5})^2}{(3-\sqrt{5})(3+\sqrt{5})}}=\sqrt{\frac{(3-\sqrt{5})^2}{3^2-5}}=\sqrt{\frac{(3-\sqrt{5})^2}{4}}=\sqrt{(\frac{3-\sqrt{5}}{2})^2}=|\frac{3-\sqrt{5}}{2}|=\frac{3-\sqrt{5}}{2}\)
AH
Akai Haruma
Giáo viên
19 tháng 7 2021
Bài 2.
a.
\(=\frac{\sqrt{8}(\sqrt{5}+\sqrt{3})}{(\sqrt{5}-\sqrt{3})(\sqrt{5}+\sqrt{3})}=\frac{2\sqrt{2}(\sqrt{5}+\sqrt{3})}{5-3}=\sqrt{2}(\sqrt{5}+\sqrt{3})=\sqrt{10}+\sqrt{6}\)
b.
\(=\sqrt{\frac{(2-\sqrt{3})^2}{(2-\sqrt{3})(2+\sqrt{3})}}=\sqrt{\frac{(2-\sqrt{3})^2}{2^2-3}}=\sqrt{(2-\sqrt{3})^2}=|2-\sqrt{3}|=2-\sqrt{3}\)
TD
0
12 tháng 7 2021
5) Ta có: \(\dfrac{\left(5\sqrt{3}+\sqrt{50}\right)\left(5-\sqrt{24}\right)}{\sqrt{75}-5\sqrt{2}}\)
\(=\dfrac{5\left(\sqrt{3}+\sqrt{2}\right)\left(\sqrt{3}-\sqrt{2}\right)^2}{5\left(\sqrt{3}-\sqrt{2}\right)}\)
=1
