Nếu sữa trong một hộp sữa có khối lượng tịnh 397 gam và thể tích 0,314 lít thì trọng lượng riêng của sữa là bao nhiêu?
A. 1,264 N/ m3.
B. 0,791 N/ m3.
C. 12 643 N/ m3.
D. 1264 N/ m3.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đổi: 397 g = 0 , 397 k g ; 0 , 314 l = 0 , 000314 m 3
Trọng lượng riêng của vật được tính theo công thức là: d = P V = 10 m V = 10.0 , 397 0 , 000314 ≈ 12643 N / m 3
Đáp án: C

Đổi m = 397 g = 0,397 kg
V = 0,314 lít = 0,000314 m 3
Trọng lượng riêng của sữa:
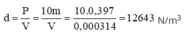
Đáp án C

Đổi: \(387g=0,387kg\)
\(V=0,314l=0,314dm^3=3,14\cdot10^{-4}\left(m^3\right)\)
a)Trọng lượng của hộp sữa:
\(P=10m=10\cdot0,387=3,87N\)
b)Trọng lượng riêng của sữa:
\(d=\dfrac{P}{V}=\dfrac{3,87}{3,14\cdot10^{-4}}=12324,84076\)(N/m3)
Khối lượng riêng:
\(d=10D\Rightarrow D=\dfrac{d}{10}=1232,484076\)(kg/m3)

Ta có: Thể tích của lon sữa là: \(V=\pi R^2h=500cm^2\)
\(\Rightarrow h=\frac{500}{\pi R^2}\)
Mặt khác: Diện tích toàn phần của lon sữa: \(S_{tp}=S_{xp}+S_d=2\pi Rh=2\pi R.R+h\)
=> Diện tích toàn phần của lon sữa đạt giá trị nhỏ nhất <=> R.R+h * đạt giá trị nhỏ nhất
Thay \(h=\frac{500}{\pi R^2}\)vào * ta được:
\(R.R+h=R.R+\frac{500}{\pi R^2}=R^2+\frac{500}{\pi R^2}=R^2+\frac{500}{2\pi R}+\frac{500}{2\pi R}\ge3.\sqrt[3]{R^2.\frac{500}{2\pi R}.\frac{500}{2\pi R}}=75.\sqrt[3]{\frac{4}{\pi^2}}\)
Áp dụng BĐT Cô-si:
Do đó: \(Min_{R.R+h}=75.\sqrt[3]{\frac{4}{\pi^2}}\)khi \(R=5\sqrt[3]{\frac{2}{\pi}};h=10\sqrt[3]{\frac{2}{\pi}}\)
Đến đây là dễ rồi nhỉ?

Khối lượng riêng của sữa là:
\(D=\dfrac{m}{V}=\dfrac{390}{0,3}=1300\) (g/l)
⇒ Chọn C
c
C