cho tam giác abc vuông tại a có ac 8cm bc=10cm kẻ trung tuyến am và phân giác ad a)tính am và diên tích tam giác abc b) tính db và dc
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABC vuông tại A có
\(BC=\dfrac{AB}{\dfrac{1}{2}}=\dfrac{10}{\dfrac{1}{2}}=20\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC=10\sqrt{3}\left(cm\right)\)

Vì AB^2 + AC^2 = BC^2 ( 6^2 + 8^2 = 10^2 )
=> ΔABC vuông tại A
a. Vì Am là trung tuyến của BC
=> AM =1/2 BC
=> AM = 5cm.
b. Xét tứ giác ADME, ta có:
góc DAE + góc AEM + góc EMD + góc MDA = 360°
=> 90° + 90° + góc EMD + 90° = 360°
=> góc EMD = 90°
=> Tứ giác ADME là hình chữ nhật.
Vì AB^2 + AC^2 = BC^2 ( 6^2 + 8^2 = 10^2 )
=> ΔABC vuông tại A
a. Vì Am là trung tuyến của BC
=> AM =1/2 BC
=> AM = 5cm.
b. Xét tứ giác ADME, ta có:
góc DAE + góc AEM + góc EMD + góc MDA = 360°
=> 90° + 90° + góc EMD + 90° = 360°
=> góc EMD = 90°
=> Tứ giác ADME là hình chữ nhật.

a) Do MN//AB nên theo Đl Ta-let ta có AM/MB=AN/NC
=>2/3=AN/9 => AN=6cm
khi đó NC= AC-NA = 9-6= 3cm
b) Áp dụng tính chất đường p/g trong tam giác ta có BD/AB=DC/AC
Do BD+DC = BC = 10cm
Áp dụng tính chất dãy tỉ số bằng nhau ta có
BD/AB = DC/AC = (BD+DC)/(AB+AC) = 10/15 = 2/3
Do đó DB/6 = 2/3 => DB = 4 cm
DC/9 =2/3 => DC = 6cm
Vậy DB = 4 cm, DC = 6 cm

a: AC=căn 10^2-6^2=8cm
BD là phân giác
=>DA/AB=DC/BC
=>DA/3=DC/5=8/8=1
=>DA=3cm; DC=5cm
b: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
góc C chung
=>ΔABC đồng dạng với ΔHAC
=>AB/HA=BC/AC
=>AB*AC=AH*BC
c: S HAC=1/2*HA*HC=1/2*4,8*6,4=15,36cm2

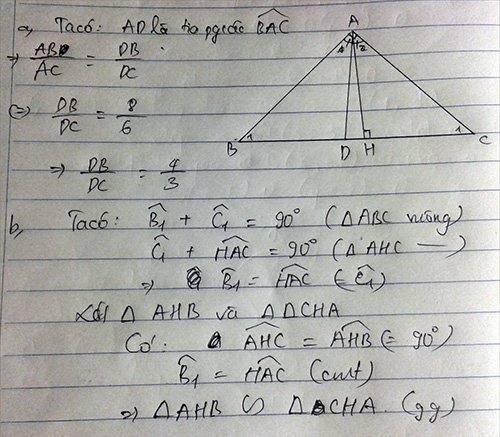

a, Vì tam giác ABC vuông tại A, M là trung điểm BC
=? AM = MB = MC = BC/2 = 5 cm
Theo định lí Pytago tam giác ABC vuông tại A
\(AB=\sqrt{BC^2-AC^2}=6cm\)
Diện tích tam giác ABC là\(S_{ABC}=\frac{1}{2}.AB.AC=\frac{1}{2}.6.8=24cm^2\)
b, Vì AD là đường phân giác nên \(\frac{AB}{AC}=\frac{DB}{DC}\Rightarrow\frac{DC}{AC}=\frac{DB}{AB}\)
Theo tc dãy tỉ số bằng nhau
\(\frac{DC}{8}=\frac{DB}{6}=\frac{DC+DB}{14}=\frac{10}{14}=\frac{5}{7}\Rightarrow DC=\frac{40}{7}cm;DB=\frac{30}{7}cm\)