tìm \(x\in Z\) \(\)sao cho
\(\dfrac{-1}{5}\le\dfrac{x}{40}< \dfrac{-1}{8}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
3
8 tháng 6 2021
`-1/5<=x/8<=1/4`
`=>8* -1/5<=x<=1/4*8`
`=>-8/5<=x<=2`
Mà `x in ZZ`
`=>x in {-1,0,1,2}`
8 tháng 6 2021
−1/5≤x8≤1/4-15≤x8≤14
⇒8⋅−1/5≤x≤14⋅8⇒8⋅-15≤x≤14⋅8
⇒−85≤x≤2⇒-85≤x≤2
Mà x∈Zx∈ℤ
⇒x∈{−1,0,1,2}
S
20 tháng 4 2023
\(-\dfrac{1}{8}< \dfrac{x}{72}\le-\dfrac{1}{36}\)
\(\Rightarrow\dfrac{-9}{72}< \dfrac{x}{72}\le-\dfrac{2}{72}\)
\(\Rightarrow x\in\left\{-8;-7;-6;-5;-4;-3;-2\right\}\)
4 tháng 12 2023
1, để \(\dfrac{2x+1}{x+3}\) là 1 số nguyên
= > 2x + 1 chia hết cho x + 3 ( x thuộc Z và x \(\ne3\) )
= > 2 ( x + 3 ) - 5 chia hết cho x + 3
=> -5 chia hết cho x + 3
hay x + 3 thuộc Ư(-5 ) \(\in\left\{\pm1;\pm5\right\}\)
Đến đây em tự tìm các giá trị của x
2, Tương tự câu 1, x - 1 chia hết cho x + 5 ( x thuộc Z và x khác - 5 )
= > - 6 chia hết cho x + 5
= > \(x+5\in\left\{\pm1;\pm2;\pm3;\pm6\right\}\)
....
3, ( x - 1 ) ( y - 3 ) = 7
x,y thuộc Z = > x - 1 ; y - 3 thuộc Ư(7)
và ( x - 1 )( y - 3 ) = 7
( 1 ) \(\left\{{}\begin{matrix}x-1=1\\y-3=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=10\end{matrix}\right.\)
(2) \(\left\{{}\begin{matrix}x-1=7\\y-3=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=8\\y=4\end{matrix}\right.\)
( 3) \(\left\{{}\begin{matrix}x-1=-1\\y-3=-7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=-4\end{matrix}\right.\)
( 4 ) \(\left\{{}\begin{matrix}x-1=-7\\y-3=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-6\\y=2\end{matrix}\right.\)
Từ ( 1 ) , ( 2 ) , ( 3 ) , ( 4 ) các cặp giá trị ( x,y ) nguyên cần tìm là ....
H
1
31 tháng 8 2021
Ai giúp mình với
Mình đăng trên OLM mà không ai giúp
Lên hỏi đáp 247 cũng không có gì
Đành lên đây
Mọi người giúp mình với 
21 tháng 1 2018
Ai lm giúp mk vs câu nào cũng được. Ai làm xong sớm nhất sẽ được tick
31 tháng 12 2021
\(c,P=\dfrac{x^2-x^2+8xy-16y^2}{x^2+4y^2}=\dfrac{8\left(\dfrac{x}{y}\right)-16}{\left(\dfrac{x}{y}\right)^2+4}\)
Đặt \(\dfrac{x}{y}=t\)
\(\Leftrightarrow P=\dfrac{8t-16}{t^2+4}\Leftrightarrow Pt^2+4P=8t-16\\ \Leftrightarrow Pt^2-8t+4P+16=0\)
Với \(P=0\Leftrightarrow t=2\)
Với \(P\ne0\Leftrightarrow\Delta'=16-P\left(4P+16\right)\ge0\)
\(\Leftrightarrow-P^2-4P+4\ge0\Leftrightarrow-2-2\sqrt{2}\le P\le-2+2\sqrt{2}\)
Vậy \(P_{max}=-2+2\sqrt{2}\Leftrightarrow t=\dfrac{4}{P}=\dfrac{4}{-2+2\sqrt{2}}=2+\sqrt{2}\)
\(\Leftrightarrow\dfrac{x}{y}=2+2\sqrt{2}\)
22 tháng 5 2022
a: \(\Leftrightarrow\dfrac{1}{2}-\dfrac{1}{2}+\dfrac{3}{2}\le x\le\dfrac{37}{24}-\dfrac{3-16}{24}=\dfrac{37-3+16}{24}=\dfrac{50}{24}=\dfrac{25}{12}\)
=>3/2<=x<=25/12
mà x là số nguyên
nên x=2
b: \(\Leftrightarrow-\dfrac{1}{23}-\dfrac{3}{23}-\dfrac{7}{23}< x\le\dfrac{1}{23}-\dfrac{8}{23}\)
=>-11<x<=-7
mà x là số nguyên
nên \(x\in\left\{-10;-9;-8;-7\right\}\)
6 tháng 3 2017
b, \(\dfrac{x-3}{4}=\dfrac{15}{20}\)
<=> \(\dfrac{x-3}{4}=\dfrac{3}{4}\)
=> x-3=3
<=> x=6
Vậy x=6
TT
9 tháng 6 2017
\(a,\dfrac{x}{15}=\dfrac{4}{y}=\dfrac{-2}{5}\)
* \(\dfrac{x}{15}=\dfrac{-2}{5}\)
\(\Rightarrow\dfrac{x}{15}=\dfrac{-6}{15}\)
\(\Rightarrow x=-6\)
*\(\dfrac{4}{y}=\dfrac{-2}{5}\)
\(\Rightarrow\dfrac{4}{y}=\dfrac{4}{-10}\)
\(\Rightarrow y=-10\)
Vậy x = - 6 ; y = - 10
\(b,\dfrac{x-3}{4}=\dfrac{15}{20}\)
=> ( x - 3 ) . 20 = 4. 15
=> 20x - 60 = 60
=> 20x = 60 + 60
=> 20x = 120
=> x = 120 : 20
=> x = 6
Vậy x = 6
\(c,\dfrac{-5}{9}+\dfrac{-8}{15}+\dfrac{22}{-9}+\dfrac{-7}{15}< x\le\dfrac{-1}{3}+\dfrac{-1}{4}+\dfrac{-5}{12}\)
\(\Rightarrow\dfrac{-5}{9}+\dfrac{-8}{15}+\dfrac{-22}{9}+\dfrac{-7}{15}< x\le\dfrac{-4}{12}+\dfrac{-3}{12}+\dfrac{-5}{12}\)
\(\Rightarrow\left(\dfrac{-5}{9}+\dfrac{-22}{9}\right)+\left(\dfrac{-8}{15}+\dfrac{-7}{15}\right)< x\le-1\)
\(\Rightarrow-3+\left(-1\right)< x\le-1\)
\(\Rightarrow-4< x\le-1\)
\(\Rightarrow x=-3;-2;-1\)
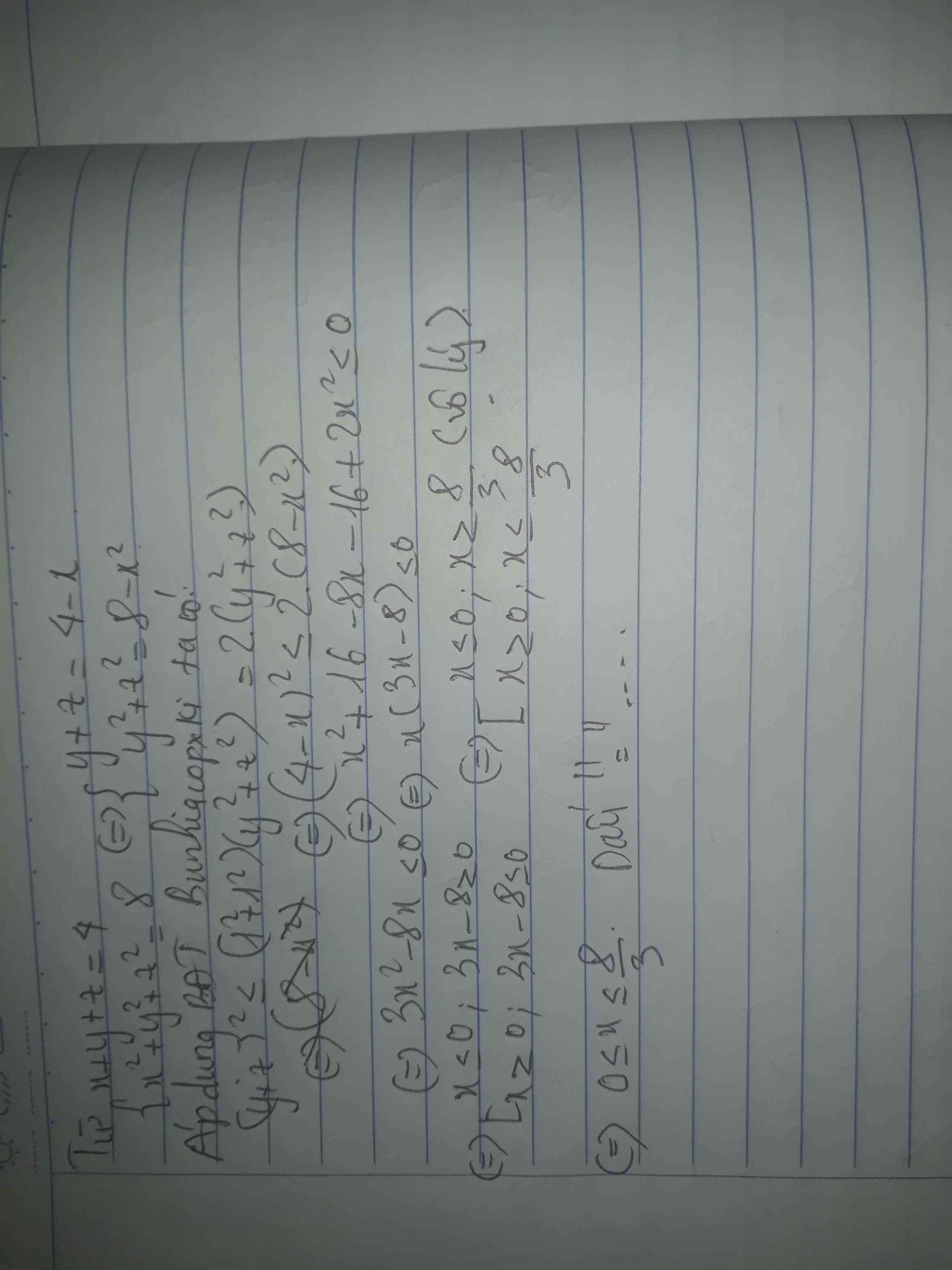
\(\dfrac{-1}{5}\le\dfrac{x}{40}\le\dfrac{-1}{8}\)
\(\Leftrightarrow\dfrac{-8}{40}\le\dfrac{x}{40}\le\dfrac{-5}{40}\)
\(\Leftrightarrow-8\le x\le-5\)
Mà x\(\in Z\)
\(\Rightarrow x\in\left\{-8;-7;-6;-5\right\}\)
Vậy ...
ủa hình như hơi sai sai