Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bài làm :
a) Xét tam giác BEM và tam giác CFM
Ta có: BM = MC ( vì M là trung điểm của BC)
M là góc chung
Do đó : tam giác BEM=CFM( cạnh huyền- góc nhọn)
b) Bạn ghi chưa hết đề nên mik ko hiểu
sorry 
a: Xét tứ giác AEMF có
\(\widehat{AEM}=\widehat{AFM}=\widehat{FAE}=90^0\)
Do đó: AEMF là hình chữ nhật
Suy ra: AM=EF
b: \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{6\cdot8}{2}=24\left(cm^2\right)\)
=>AH=4,8cm
c: Xét ΔABC có
M là trung điểm của BC
ME//AC
Do đó: E là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
MF//AB
Do đó: F là trung điểm của AC
Ta có: ΔAHC vuông tại H
mà HF là đường trung tuyến
nên HF=AC/2=AF
mà AF=ME
nên HF=ME
Xét ΔABC có
E là trung điểm của AB
F là trung điểm của AC
Do đó: FE là đường trung bình
=>FE//BC
Xét tứ giác EHMF có
MH//FE
Do đó: EHMF là hình thang
mà EM=HF
nên EHMF là hình thang cân
a./ \(\Delta BEM=\Delta CFM\)vì:
b./ => ME = MF (cạnh tương ứng của 2 tam giác bằng nhau) => M nằm trên trung trực của EF (vì cách đều 2 đầu của EF) (1)
\(\Delta BEM=\Delta CFM\)=> BE = CF => AE = AF ( vì cùng bằng AB - BE = AC - CF)
=> A nằm trên trung trực của EF (vì cách đều 2 đầu của EF) (2)
Từ (1) (2) => AM là trung trực của EF.
a, Vì Tam giác `ABC` cân tại A `=> AB = AC ;`\(\widehat{B}=\widehat{C}\)
Xét Tam giác `AMB` và Tam giác `AMC` có:
`AM chung`
\(\widehat{B}=\widehat{C}\) `(CMT)`
`MB = MC (g``t)`
`=>` Tam giác `AMB =` Tam giác `AMC (c-g-c)`
b, Vì Tam giác `AMB =` Tam giác `AMC (a)`
`=>` \(\widehat{EAM}=\widehat{FAM}\) (2 góc tương ứng).
Xét Tam giác `EAM` và Tam giác `FAM` có:
AM chung
\(\widehat{EAM}=\widehat{FAM}\) `(CMT)`
\(\widehat{AEM}=\widehat{AFM}=90^0\)
`=>` Tam giác `EAM =` Tam giác `FAM (ch-gn)`
`=> EA = FA` (2 cạnh tương ứng).
c, *câu này mình hơi bí bn ạ:')
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
Do đó: ΔAEM=ΔAFM
=>AE=AF
c: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
a) xét ΔABM và ΔACM có
góc B = góc C
AB = AC ( ΔABC cân tại A )
BM=CM ( tính chất các đường của Δ cân từ đỉnh )
=> ΔABM = ΔACM
b) xét ΔBME và ΔCMF có
góc B bằng góc C
BM=CM
=> ΔBME=ΔCMF ( cạnh huyền góc nhọn )
=> FM = EM
=> ΔEMF cân tại M
c) gọi giao của EF và AM là O
ta có BE = CF => AE=AF
=> ΔAEF cân tại A
ta có AM là tia phân giác của góc A
mà O nằm trên AM suy ra AO cũng là tia phân giác của góc A
ta lại có ΔAEF cân tại A
suy ra AO vuông góc với EF
suy ra AM vuông góc với EF
xét ΔAEF và ΔABC có
EF và BC đều cùng vuông góc với AM => EF // BC
a) Xét ΔABM và ΔACM có
AB=AC(ΔABC cân tại A)
AM chung
BM=CM(M là trung điểm của BC)
Do đó: ΔABM=ΔACM(c-c-c)
b) Xét ΔEMB vuông tại E và ΔFMC vuông tại F có
BM=CM(M là trung điểm của BC)
\(\widehat{EBM}=\widehat{FCM}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔEMB=ΔFMC(Cạnh huyền-góc nhọn)
Suy ra: ME=MF(hai cạnh tương ứng)
Xét ΔEMF có ME=MF(cmt)
nên ΔEMF cân tại M(Định nghĩa tam giác cân)
a) Xét tam giác BEM và tam giácCFM
có:BM=MC(gt)
góc EBM=gócFCM(tam giác ABC can^)
->T/g BEM=t/g CFM(c.huyền g. nhon)
b)
Xét tam giác vg AEM va t/g vg AFM
có:EM=MF(t/g BEM=t/gAFM)
AM là cạnh chung
->t/g AEM =t/g AFM( c/ huyền -c.góc vg)
->AE=AF(2 cạnh tương ứng)
Xét tam giác AEI và t/g AFI
có:MF=EM(t/g BEM= t/g CFM)
AM là cạnh chung
AF=AE(C/ m trên)
->t/g AEI =t/g AFI(c-c-c)
->EI = IF(2 cạnh tương ứng)
->góc AIE= góc AIF(2 tương ứng)
=>AE là đường trung trực của EF
c(mik ko pt lm)
a và b bạn Hương Sơn
c) Ta có:
\(\Delta ABC\)cân
có AM là đường trung tuyến
=> AM cũng là đường trung trực
=> \(AM\perp BC\)
=> AM = 90 độ
Vì \(\Delta ABC\)cân
=> Góc ABM = góc ACM (1)
mà Góc ABD = góc ACD = 90 độ (2)
Từ (1) và (2) => Góc MBD = góc MCD
Xét \(\Delta DMB\)và \(\Delta DMC\)có :
DM : cạnh chung (1)
Góc MBD = góc MCD ( chứng minh trên ) (2)
BM = MC ( vì AM là đường trung tuyến của tam giác ABC ) (3)
Từ (1) ; (2) và (3) => \(\Delta DMB=\Delta DMC\)(cạnh - góc - cạnh)
=> Góc CMD = góc BMD ( cặp góc tương ứng)
Mà Góc CMD + góc BMD = 180 độ
=> Góc CMD = BMD = 180 : 2 = 90 độ
Vì Góc AMC = 90 độ ( vì AM là đường trung trực)
và góc CMD = 90 độ
=> AMC + CMD = AMD
=> 90 + 90 = AMD
=> AMD = 180 độ
=> Ba điểm A ; M ; D thẳng hàng. ( điều phải chứng minh)
Chúc bạn học tốt !
và BC = a. Tính diện tich tứ giác AEMF theo a.
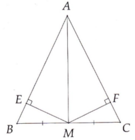
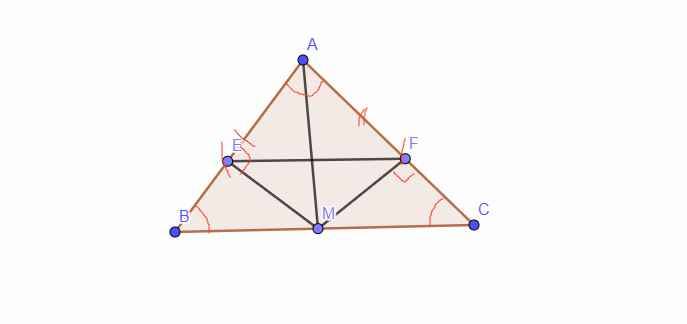
a) M là trug điểm nên AM là trug tuyến mà tg ABC cân nên AM là phân giác
tg AME và tg AMF vuông tại E và F có
am chung
EÂM=FAM ( AM là phân giác)
suy ra tg AME=AMF
b) ta có tg AEM=AMF suy ra AE=AF suy ra tg AEF cân AM là phân giác suy ra AM là đườg trug trực của tg AEF suy ra AM là đườg trug trực của EF
c) hai tg ở câu a = nhau suy ra ME=MF
xét tg EBM và tg NCM có EM=MN; BM=CM (M là trug điểm); góc EMB=FMC( đối đỉnh) suy ra hai tg = nhau suy ra góc E= N= 90 độ ( 2 góc tương ứng) mà hai góc này ở vị trí so le trog suy ra CN//AB
cho mk nhé