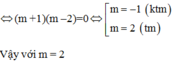Cho bt: x2-3x-m2+m+1=0. Tìm m để pt có 2 nghiệm x1, x2 thỏa mãn: 3x1+x22 +6=8m
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
\(\Delta'=\left(m+4\right)^2-\left(m^2+8m+15\right)=1>0\Rightarrow\) pt luôn có 2 nghiệm pb với mọi m
Do \(x_1< x_2\Rightarrow\left\{{}\begin{matrix}x_1=m+4-1=m+3\\x_2=m+4+1=m+5\end{matrix}\right.\)
\(3x_1-2x_2=15\)
\(\Leftrightarrow3\left(m+3\right)-2\left(m+5\right)=15\)
\(\Leftrightarrow m=16\)
BL
1
Y
1 tháng 4 2023
\(x^2+2\left(m+1\right)+4m-4=0\)
Theo Vi - ét, ta có :
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-2\left(m+1\right)\\x_1x_2=\dfrac{c}{a}=4m-4\end{matrix}\right.\)
Ta có :
\(x_1^2+x_2^2+3x_1x_2=0\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2+3x_1x_2=0\)
\(\Leftrightarrow\left(x_1+x_2\right)^2+x_1x_2=0\)
\(\Leftrightarrow\left[-2\left(m+1\right)\right]^2+\left(4m-4\right)=0\)
\(\Leftrightarrow4\left(m^2+2m+1\right)+4m-4=0\)
\(\Leftrightarrow4m^2+8m+4+4m-4=0\)
\(\Leftrightarrow4m^2+12m=0\)
\(\Leftrightarrow4m\left(m+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=-3\end{matrix}\right.\)
S
1
NV
30 tháng 3 2023
\(x^2-2x-m^2+m-4=0\left(1\right)\)
Để phương trình (1) có 2 nghiệm phân biệt thì:
\(\Delta>0\Rightarrow\left(-2\right)^2-4.\left(-m^2+m-4\right)>0\)
\(\Rightarrow4+4m^2-4m+16>0\)
\(\Leftrightarrow\left(2m-1\right)^2+19>0\) (luôn đúng)
Vậy với \(\forall m\) thì phương trình (1) luôn có 2 nghiệm phân biệt.
Theo định lí Viete cho phương trình (1) ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1x_2=-m^2+m-4\end{matrix}\right.\)
Ta có: \(\left|3x_1\right|-\left|x_2\right|=6\left(2\right)\)
Ta thấy:\(-m^2+m-4=-\left(m^2-m+\dfrac{1}{4}\right)-\dfrac{15}{4}=-\left(m-\dfrac{1}{2}\right)^2-\dfrac{15}{4}\le-\dfrac{15}{4}< 0\)
\(\Rightarrow-m^2+m-4< 0\) hay \(x_1x_2< 0\). Do đó x1, x2 phải trái dấu.
Ta xét 2 trường hợp:
TH1, x1>0 , x2<0. Khi đó:
\(\left(2\right)\Rightarrow3x_1+x_2=6\)
\(\Rightarrow\left(x_1+x_2\right)-6=-2x_1\left(1'\right)\) và \(3\left(x_1+x_2\right)-6=2x_2\left(2'\right)\)
Lấy (1') nhân cho (2') ta được:
\(\left[\left(x_1+x_2\right)-6\right]\left[3\left(x_1+x_2\right)-6\right]=-4x_1x_2\)
\(\Rightarrow\left(-2-6\right)\left[3.\left(-2\right)-6\right]=-4\left(-m^2+m-4\right)\)
\(\Leftrightarrow-m^2+m-4=-24\)
\(\Leftrightarrow m^2-m+4=24\)
\(\Leftrightarrow m^2-m-20=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=5\\m=-4\end{matrix}\right.\)
TH2: x1<0 ; x2>0. Khi đó:
\(\left(2\right)\Rightarrow3x_1+x_2=-6\)
\(\Rightarrow\left(x_1+x_2\right)+6=-2x_1\left(3'\right)\) và \(3\left(x_1+x_2\right)+6=2x_2\left(4'\right)\)
Lấy (3') nhân cho (4') ta được:
\(\left[\left(x_1+x_2\right)+6\right]\left[3\left(x_1+x_2\right)+6\right]=-4x_1x_2\)
\(\Rightarrow\left(-2+6\right)\left[3.\left(-2\right)+6\right]=-4\left(-m^2+m-4\right)\)
\(\Rightarrow m^2-m+4=0\) (phương trình vô nghiệm)
Thử lại ta có \(\left[{}\begin{matrix}m=5\\m=-4\end{matrix}\right.\)
VD
11 tháng 3 2022
Bài 1:
a, Thay m=-1 vào (1) ta có:
\(x^2-2\left(-1+1\right)x+\left(-1\right)^2+7=0\\
\Leftrightarrow x^2+1+7=0\\
\Leftrightarrow x^2+8=0\left(vô.lí\right)\)
Thay m=3 vào (1) ta có:
\(x^2-2\left(3+1\right)x+3^2+7=0\\ \Leftrightarrow x^2-2.4x+9+7=0\\ \Leftrightarrow x^2-8x+16=0\\ \Leftrightarrow\left(x-4\right)^2=0\\ \Leftrightarrow x-4=0\\ \Leftrightarrow x=4\)
b, Thay x=4 vào (1) ta có:
\(4^2-2\left(m+1\right).4+m^2+7=0\\ \Leftrightarrow16-8\left(m+1\right)+m^2+7=0\\ \Leftrightarrow m^2+23-8m-8=0\\ \Leftrightarrow m^2-8m+15=0\\ \Leftrightarrow\left(m^2-3m\right)-\left(5m-15\right)=0\\ \Leftrightarrow m\left(m-3\right)-5\left(m-3\right)=0\\ \Leftrightarrow\left(m-3\right)\left(m-5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=3\\m=5\end{matrix}\right.\)
c, \(\Delta'=\left[-\left(m+1\right)\right]^2-\left(m^2+7\right)=m^2+2m+1-m^2-7=2m-6\)
Để pt có 2 nghiệm thì \(\Delta'\ge0\Leftrightarrow2m-6\ge0\Leftrightarrow m\ge3\)
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=2m+2\\x_1x_2=m^2+7\end{matrix}\right.\)
\(x_1^2+x_2^2=0\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=0\\ \Leftrightarrow\left(2m+2\right)^2-2\left(m^2+7\right)=0\\ \Leftrightarrow4m^2+8m+4-2m^2-14=0\\ \Leftrightarrow2m^2+8m-10=0\\ \Leftrightarrow\left[{}\begin{matrix}m=1\left(ktm\right)\\m=-5\left(ktm\right)\end{matrix}\right.\)
\(x_1-x_2=0\\ \Leftrightarrow\left(x_1-x_2\right)^2=0\\ \Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=0\\ \Leftrightarrow\left(2m+2\right)^2-4\left(m^2+7\right)=0\\ \Leftrightarrow4m^2+8m+4-4m^2-28=0\\ \Leftrightarrow8m=28=0\\ \Leftrightarrow m=\dfrac{7}{2}\left(tm\right)\)
VD
11 tháng 3 2022
Bài 2:
a,Thay m=-2 vào (1) ta có:
\(x^2-2x-\left(-2\right)^2-4=0\\ \Leftrightarrow x^2-2x-4-4=0\\ \Leftrightarrow x^2-2x-8=0\\ \Leftrightarrow\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\)
b, \(\Delta'=\left(-m\right)^2-\left(-m^2-4\right)\ge0=m^2+m^2+4=2m^2+4>0\)
Suy ra pt luôn có 2 nghiệm phân biệt
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=-m^2-4\end{matrix}\right.\)
\(x_1^2+x_2^2=20\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=20\\ \Leftrightarrow2^2-2\left(-m^2-4\right)=20\\ \Leftrightarrow4+2m^2+8-20=0\\ \Leftrightarrow2m^2-8=0\\ \Leftrightarrow m=\pm2\)
\(x_1^3+x_2^3=56\\ \Leftrightarrow\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=56\\ \Leftrightarrow2^3-3\left(-m^2-4\right).2=56\\ \Leftrightarrow8-6\left(-m^2-4\right)-56\\ =0\\ \Leftrightarrow8+6m^2+24-56=0\\ \Leftrightarrow6m^2-24=0\\ \Leftrightarrow m=\pm2\)
\(x_1-x_2=10\\ \Leftrightarrow\left(x_1-x_2\right)^2=100\\ \Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2-100=0\\ \Leftrightarrow2^2-4\left(-m^2-4\right)-100=0\\ \Leftrightarrow4+4m^2+16-100=0\\ \Leftrightarrow4m^2-80=0\\ \Leftrightarrow m=\pm2\sqrt{5}\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 2 2021
\(\Delta=9-4\left(-m^2+m+2\right)=4m^2-4m+1=\left(2m-1\right)^2\)
Pt có 2 nghiệm pb khi \(m\ne\dfrac{1}{2}\)
Do vai trò của 2 nghiệm là như nhau, giả sử: \(\left\{{}\begin{matrix}x_1=\dfrac{3-\left(2m-1\right)}{2}=2-m\\x_2=\dfrac{3+2m-1}{2}=m+1\end{matrix}\right.\)
\(x_1^2+x_2^2=5\Leftrightarrow\left(2-m\right)^2+\left(m+1\right)^2=5\)
\(\Leftrightarrow m^2-m=0\Rightarrow\left[{}\begin{matrix}m=0\\m=1\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
17 tháng 3 2021
Lời giải:
Để PT có 2 nghiệm $x_1,x_2$ thì:
$\Delta'=(m+1)^2-(m^2-1)>0\Leftrightarrow 2m+2>0\Leftrightarrow m>-1$
Áp dụng định lý Viet:
$x_1+x_2=2(m+1)$ và $x_1x_2=m^2-1$
Khi đó, để $x_1^2+x_2^2=x_1x_2+8$
$\Leftrightarrow (x_1+x_2)^2-2x_1x_2=x_1x_2+8$
$\Leftrightarrow (x_1+x_2)^2=3x_1x_2+8$
$\Leftrightarrow 4(m+1)^2=3(m^2-1)+8$
$\Leftrightarrow m^2+8m-1=0$
$\Leftrightarrow m=-4\pm \sqrt{17}$. Vì $m>-1$ nên $m=-4+\sqrt{17}$
9 tháng 1 2023
Δ=(-4)^2-4(m^2+3m)
=16-4m^2-12m
=-4(m^2+3m-4)
=-4(m+4)(m-1)
Để phươg trình có hai nghiệm thì Δ>=0
=>-4(m+4)(m-1)>=0
=>(m+4)(m-1)<=0
=>-4<=m<=1
x1^2+x2^2=6
=>(x1+x2)^2-2x1x2=6
=>4^2-2(m^2+3m)=6
=>16-2m^2-6m-6=0
=>-2m^2-6m+10=0
=>m^2+3m-5=0
=>\(m=\dfrac{-3\pm\sqrt{29}}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 1 2023
\(\Delta'=4-m^2-3m\ge0\Rightarrow-4\le m\le1\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=4\\x_1x_2=m^2+3m\end{matrix}\right.\)
\(x_1^2+x_2^2=6\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=6\)
\(\Leftrightarrow4^2-2\left(m^2+3m\right)=6\)
\(\Leftrightarrow m^2+3m-5=0\Rightarrow\left[{}\begin{matrix}m=\dfrac{-3+\sqrt{29}}{2}>1\left(loại\right)\\m=\dfrac{-3-\sqrt{29}}{2}< -4\left(loại\right)\end{matrix}\right.\)
Vậy ko tồn tại m thỏa mãn yêu cầu đề bài