chung minh rang tam giac co hai duong phan giac bang nhau thitam giac do can
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét tam giác ABCABC có phân giác AN=BPAN=BP. Kẻ MN∥AB,PQ∥ABMN∥AB,PQ∥AB. Ta sẽ chứng minh PQ≡MNPQ≡MN
Thật vậy, dễ dàng chứng minh AM=MN,PQ=QBAM=MN,PQ=QB
Xét 2 tam giác cân AMNAMN và PQBPQB có cạnh đáy bằng nhau mà MN>PQMN>PQ (ko mất tính tq, giả sử MNMN gần ABAB hơn PQPQ)
⇒∠PQB>∠NMA⇒∠PQB>∠NMA
⇒∠MAB<∠NBA⇒∠MAB<∠NBA
⇒AM<BN⇒AM<BN
Mà ta lại có AM=MN>PQ=QB>BNAM=MN>PQ=QB>BN (vô lý)
⇒MN≡PQ⇒MN≡PQ
còn lai tu lam nhé!

Xét tam giác DCB và tam giác EBC có :
BC là cạnh chung
Góc CDB = góc CEB = 90 độ
BD = CE
\(\Rightarrow\) tam giác DCB = tam giác ECB (cạnh huyền góc nhọn)
\(\Rightarrow\) Góc DCB = góc EBC hay góc ACB = góc ABC
\(\Rightarrow\) Tam giác ABC cân

A B C D E O
Do O thuộc trung tuyến CD của tam giác ABC nên OC = 2/3 CD và OD = 1/3 CD
Do O thuộc trung tuyến BE của tam giác ABC nên OB = 2/3 BE và OE = 1/3 BE
Do CD = BE(theo đề ra) => 2/3 CD = 2/3 BE và 1/3 CD = 1/3 BE<=> OC = OB và OD = OE
Từ OC = OB => Tam giác BOC cân tại O => Góc OBC = Góc OCB (1)
Xét tam giác DOB và tam giác EOC có: OC = OB (chứng minh trên); Góc DOB = Góc EOC(đối đỉnh) ; OD = OE (chứng minh trên)
=> Tam giác DOB = Tam giác EOC(c.g.c) => Góc OBD = Góc OCE(2 góc tương ứng) (2)
Cộng từng vế của (1) và (2) ta được : Góc OBC + Góc OBD = Góc OCB + Góc OCE =>Góc DBC = Góc ECB
Mà A;D;B thẳng hàng và A;E;C thẳng hàng =>Góc ABC = Góc ACB =>Tam giác ABC cân tại A
Vậy nếu 1 tam giác có 2 đường trung tuyến bằng nhau thì tam giác đó là tam giác cân.
chung minh rang ba trung tuyen cua mot tam giac chia tam giac do thanh 6 phan co dien tich bang nhau


M N P H
a,C/m \(\Delta\) MNH la tam giác cân
Xét \(\Delta MNP\) :
MH là đường cao đồng thời là đường trung trực
=> \(\Delta MNP\) cân tại M
b, C/m MH là tia phân giác

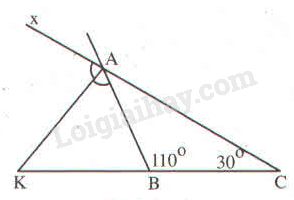
Ta có \(\widehat{xAB}\) là góc ngoài tại đỉnh A của \(\Delta ABC.\)
\(\Rightarrow\widehat{xAB}=\widehat{ABC}+\widehat{ACB}\) (tính chất góc ngoài tam giác).
\(\Rightarrow\widehat{xAB}=110^0+30^0\)
\(\Rightarrow\widehat{xAB}=140^0.\)
Vì \(AK\) là tia phân giác của \(\widehat{BAx}\left(gt\right)\)
\(\Rightarrow\widehat{xAK}=\widehat{KAB}=\frac{\widehat{BAx}}{2}=\frac{140^0}{2}=70^0\) (1)
Lại có: \(\widehat{ABC}+\widehat{ABK}=180^0\) (vì 2 góc kề bù)
\(\Rightarrow110^0+\widehat{ABK}=180^0\)
\(\Rightarrow\widehat{ABK}=180^0-110^0\)
\(\Rightarrow\widehat{ABK}=70^0\) (2)
Từ (1) và (2) \(\Rightarrow\widehat{KAB}=\widehat{ABK}=70^0.\)
Mà 2 góc này thuộc \(\Delta KAB\)
\(\Rightarrow\Delta KAB\) có 2 góc bằng nhau (đpcm).
Chúc bạn học tốt!

A B D C E
a) có AB// DC (gt)
mà E thuộc DC => AB // CE
=> \(\widehat{ABC}=\widehat{ECB}\)
có AC // BE (gt)
=>\(\widehat{ACB}=\widehat{EBC}\)
xét \(\Delta ABC\) và \(\Delta ECB\)
có BC là cạnh chung
\(\widehat{ABC}=\widehat{ECB}\) (cmt)
\(\widehat{ACB}=\widehat{EBC}\) (cmt)
=> \(\Delta ABC=\Delta ECB\) (gcg)
=>BE = CA ( 2 cạnh tương ứng )
b) có AC = BD ( gt)
mà BE = CA (cmt)
=> BD = BE ( = CA)
=>\(\Delta BDE\) là tam giác cân tại B
