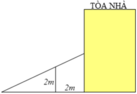
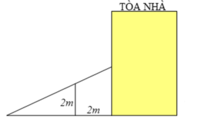
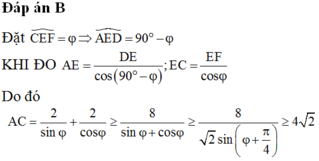
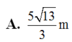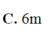một bức tường cao 8m. Người ta dựng 1 cái thang cách chân tường 6m thì đầu thang vừa chạm vào thành bức tường.Hỏi thang dài bao nhiêu mét
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 7 2023
35dm=3,5m
Chiều cao của bức tường là:
\(\sqrt{3.5^2-0.8^2}\simeq3,41\left(m\right)\)
H9
HT.Phong (9A5)
CTVHS
3 tháng 8 2023
Gọi tam giác tạo thành là tam giác ABC
Với chiếc thang là cạnh huyền AC, khoảng cách của chân thang và chân tường là BC và chiều cao của bức tường là AB:
Áp dụng định lý Py-ta-go ta có:
\(AC=\sqrt{BC^2+AB^2}=\sqrt{1,5^2+6^2}\approx6,2\left(m\right)\)
Độ dài của chiếc thang nhỏ:
\(A'C'=\dfrac{2}{3}\cdot AC=\dfrac{2}{3}\cdot6,2\approx4,13\left(m\right)\)
Áp dụng định lý Py-ta-go ta tìm được độ cao mà thang đặt đến:
\(A'B'=\sqrt{A'C'^2-B'C'^2}=\sqrt{4,13^2-1^2}\approx4\left(m\right)\)
Điểm cao nhất của thang cách mặt bước tường là:
\(AB-A'B'=6-4=2\left(m\right)\)
Vậy....
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
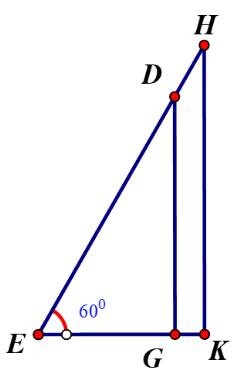
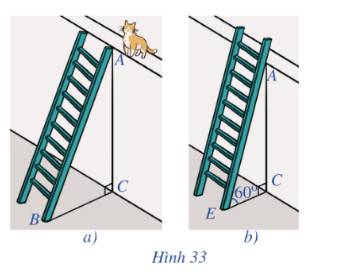
Gọi chiều cao bức tường DG là x (m) (x>0)
Chiều dài chiếc thang là x+1 (m)
Khoảng cách từ chân thang sau khi bác Nam điều chỉnh là: \(EG = \frac{{DG}}{{\sqrt 3 }} = \frac{{x\sqrt 3 }}{3}\) (m)
Áp dụng định lý Py-ta-go cho tam giác vuông ABC ta có:
\(BC = \sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} \)(m)
Bác Nam dịch chuyển chân thang vào gần chân tường thêm 0,5 m nên ta có:
\(\sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} - 0,5 = \frac{{x\sqrt 3 }}{3}\)
\(\begin{array}{l} \Leftrightarrow \sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} = \frac{x}{{\sqrt 3 }} + 0,5\\ \Leftrightarrow \sqrt {2x + 1} = \frac{x}{{\sqrt 3 }} + 0,5\left( * \right)\end{array}\)
Ta có \(\frac{x}{{\sqrt 3 }} + 0,5 \ge 0 \Leftrightarrow \frac{x}{{\sqrt 3 }} \ge - \frac{1}{2}\)\( \Leftrightarrow x \ge - \frac{{\sqrt 3 }}{2}\) (Luôn đúng do x>0)
Ta bình phương hai vế (*) ta được:
\(\begin{array}{l}2x + 1 = {\left( {\frac{x}{{\sqrt 3 }} + 0,5} \right)^2}\\ \Leftrightarrow 2x + 1 = \frac{{{x^2}}}{3} + \frac{x}{{\sqrt 3 }} + 0,25\\ \Leftrightarrow \frac{{{x^2}}}{3} + \left( {\frac{{\sqrt 3 }}{3} - 2} \right)x - \frac{3}{4} = 0\\ \Leftrightarrow \left[ \begin{array}{l}x \approx 4,7\left( {tm} \right)\\x \approx - 0,5\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy chiều cao của bức tường là 4,7 m.
10 tháng 5 2021
Vẽ tam giác ABC, BC=2,5m, AC=6,5m. ABC vuông tại B
Dịnh lí Pitago: AB=\(\sqrt{AC^2-BC^2}\) =6m