Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
1.a)\(\frac{x^3}{x^2-4}-\frac{x}{x-2}-\frac{2}{x+2}\)
\(=\frac{x^3}{\left(x+2\right)\left(x-2\right)}-\frac{x}{x-2}-\frac{2}{x+2}\)
Để biểu thức được xác định thì:\(\left(x+2\right)\left(x-2\right)\ne0\)\(\Rightarrow x\ne\pm2\)
\(\left(x+2\right)\ne0\Rightarrow x\ne-2\)
\(\left(x-2\right)\ne0\Rightarrow x\ne2\)
Vậy để biểu thức xác định thì : \(x\ne\pm2\)
b) để C=0 thì ....
1, c , bn Nguyễn Hữu Triết chưa lm xong
ta có : \(/x-5/=2\)
\(\Rightarrow\orbr{\begin{cases}x-5=2\\x-5=-2\end{cases}}\Rightarrow\orbr{\begin{cases}x=7\\x=3\end{cases}}\)
thay x = 7 vào biểu thứcC
\(\Rightarrow C=\frac{4.7^2\left(2-7\right)}{\left(7-3\right)\left(2+7\right)}=\frac{-988}{36}=\frac{-247}{9}\)KL :>...
thay x = 3 vào C
\(\Rightarrow C=\frac{4.3^2\left(2-3\right)}{\left(3-3\right)\left(3+7\right)}\)
=> ko tìm đc giá trị C tại x = 3
a: \(A=\left(\dfrac{x}{x^2-4}+\dfrac{4}{x-2}+\dfrac{1}{x+2}\right):\dfrac{3x+3}{x^2+2x}\)
\(=\dfrac{x+4x+8+x-2}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x\left(x+2\right)}{3\left(x+1\right)}\)
\(=\dfrac{6\left(x+1\right)\cdot x\left(x+2\right)}{3\left(x+1\right)\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x}{x-2}\)
a) ĐKXĐ: \(x\notin\left\{3;-3;-2\right\}\)
Ta có: \(P=\left(\dfrac{2x-1}{x+3}-\dfrac{x}{3-x}-\dfrac{3-10x}{x^2-9}\right):\dfrac{x+2}{x-3}\)
\(=\left(\dfrac{\left(2x-1\right)\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}+\dfrac{x\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}-\dfrac{3-10x}{\left(x-3\right)\left(x+3\right)}\right):\dfrac{x+2}{x-3}\)
\(=\dfrac{2x^2-6x-x+3+x^2+3x-3+10x}{\left(x-3\right)\left(x+3\right)}:\dfrac{x+2}{x-3}\)
\(=\dfrac{3x^2+6x}{\left(x-3\right)\left(x+3\right)}:\dfrac{x+2}{x-3}\)
\(=\dfrac{3x\left(x+2\right)}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{x-3}{x+2}\)
\(=\dfrac{3x}{x+3}\)
b) Ta có: \(x^2-7x+12=0\)
\(\Leftrightarrow x^2-3x-4x+12=0\)
\(\Leftrightarrow x\left(x-3\right)-4\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\left(loại\right)\\x=4\left(nhận\right)\end{matrix}\right.\)
Thay x=4 vào biểu thức \(P=\dfrac{3x}{x+3}\), ta được:
\(P=\dfrac{3\cdot4}{4+3}=\dfrac{12}{7}\)
Vậy: Khi \(x^2-7x+12=0\) thì \(P=\dfrac{12}{7}\)
a, ĐK: \(\hept{\begin{cases}x+2\ne0\\x\ne0\end{cases}\Rightarrow}\hept{\begin{cases}x\ne-2\\x\ne0\end{cases}}\)
b, \(B=\left(1-\frac{x^2}{x+2}\right).\frac{x^2+4x+4}{x}-\frac{x^2+6x+4}{x}\)
\(=\frac{-x^2+x+2}{x+2}.\frac{\left(x+2\right)^2}{x}-\frac{x^2+6x+4}{x}\)
\(=\frac{\left(-x^2+x+2\right)\left(x+2\right)-\left(x^2+6x+4\right)}{x}\)
\(=\frac{-x^3-2x^2+x^2+2x+2x+4-\left(x^2+6x+4\right)}{x}\)
\(=\frac{-x^3-2x^2-2x}{x}=-x^2-2x-2\)
c, x = -3 thỏa mãn ĐKXĐ của B nên với x = -3 thì
\(B=-\left(-3\right)^2-2.\left(-3\right)-2=-9+6-2=-5\)
d, \(B=-x^2-2x-2=-\left(x^2+2x+1\right)-1=-\left(x+1\right)^2-1\le-1\forall x\)
Dấu "=" xảy ra khi \(x+1=0\Rightarrow x=-1\)
Vậy GTLN của B là - 1 khi x = -1
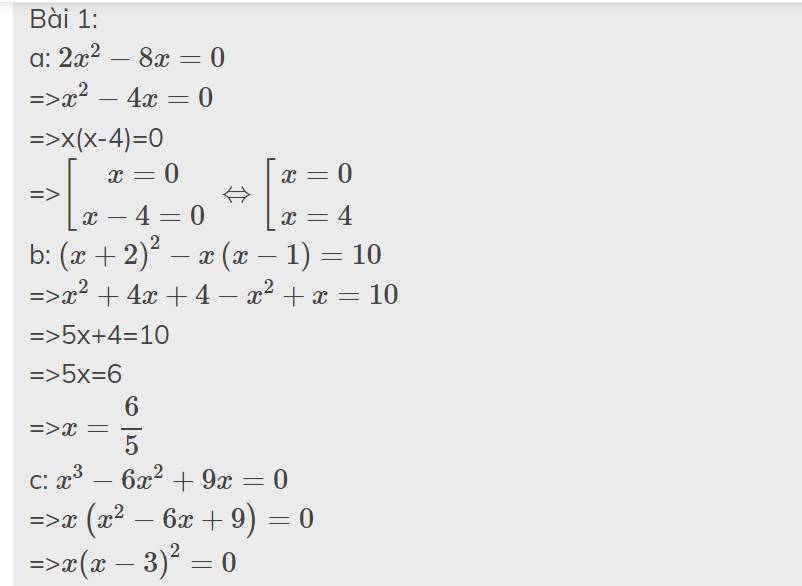
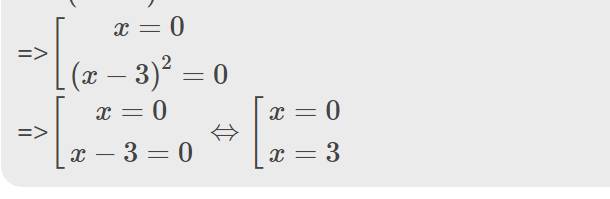Bài 2:
a: ĐKXĐ: \(x\notin\left\{0;-1;\dfrac{1}{2}\right\}\)
b: \(D=\left(\dfrac{x+2}{3x}+\dfrac{2}{x+1}-3\right):\dfrac{2-4x}{x+1}-\dfrac{3x-x^2+1}{3x}\)
\(=\dfrac{\left(x+2\right)\left(x+1\right)+6x-3\cdot3x\left(x+1\right)}{3x\left(x+1\right)}\cdot\dfrac{x+1}{2-4x}+\dfrac{x^2-3x-1}{3x}\)
\(=\dfrac{x^2+3x+2+6x-9x^2-9x}{3x}\cdot\dfrac{1}{2-4x}+\dfrac{x^2-3x-1}{3x}\)
\(=\dfrac{-8x^2+2}{3x}\cdot\dfrac{1}{-4x+2}+\dfrac{x^2-3x-1}{3x}\)
\(=\dfrac{-2\left(2x-1\right)\left(2x+1\right)}{3x\cdot\left(-2\right)\left(2x-1\right)}+\dfrac{x^2-3x-1}{3x}\)
\(=\dfrac{2x+1}{3x}+\dfrac{x^2-3x-1}{3x}\)
\(=\dfrac{2x+1+x^2-3x-1}{3x}=\dfrac{x^2-x}{3x}=\dfrac{x-1}{3}\)
c: Khi x=1 thì \(D=\dfrac{1-1}{3}=0\)
a: ĐKXĐ: \(x\notin\left\{1;-1\right\}\)
b: \(P=\dfrac{x}{2\left(x-1\right)}-\dfrac{x^2+1}{2\left(x-1\right)\left(x+1\right)}=\dfrac{x^2+x-x^2-1}{2\left(x-1\right)\left(x+1\right)}=\dfrac{1}{2x+2}\)
Đề bài là \(B=\dfrac{\left(x-1\right)^2-4}{\left(2x+1\right)^2-\left(x+2\right)^2}\) hay là \(B=\dfrac{\left(x-1\right)^2-4}{\left(2x+1\right)^2}-\left(x+2\right)^2?\)
\(\dfrac{\left(x-1\right)^2-4}{\left(2x+1\right)^2-\left(x+2\right)^2}\)
viết lại biểu thức