Cho tam giác ABC cân tại A.Đường cao AH,biết AB=5cm,BC=6cm.Tính độ dài đoạn thẳng BH,Ah
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
30 tháng 9 2018
a, HB = 1,8cm; CH = 3,2cm; AH = 2,4cm; AC = 4cm
b, AB = 65cm; AC = 156cm; BC = 169cm; BH = 25cm
c, AB = 5cm; BC = 13cm; BH = 25/13cm; CH = 144/13cm
3 tháng 5 2021
a) △ABC cân tại A có AH là đường cao
⇒ AH là đường trung tuyến
\(\Rightarrow BH=\dfrac{1}{2}BC=\dfrac{1}{2}.6=3\left(cm\right)\)
△AHB vuông tại H có \(AB^2=AH^2+HB^2\\ \Rightarrow AH=\sqrt{AB^2-HB^2}=\sqrt{5^2-3^2}=4\left(cm\right)\)
b) △ABC có AH là đường trung tuyến
G là trọng tâm
\(\Rightarrow G\in AH\) hay A; G; H thẳng hàng
c) △ABC cân tại A có AH là đường cao
⇒ AH là đường phân giác
\(\Rightarrow\widehat{BAH}=\widehat{CAH}\)
△ABG và △ACG có:
\(AB=AC\\ \widehat{BAG}=\widehat{CAG}\\ AG:\text{cạnh chung}\)
\(\Rightarrow\text{△ABG = △ACG}\left(c.g.c\right)\)
\(\Rightarrow\widehat{ABG}=\widehat{ACG}\)
NL
2
14 tháng 3 2017
xét tg ABH va tg ACH, có
AHB=AHC(=90đ)
AB=AC(tg ABC cân tại a)
AH cạnh chung
Do đó, tg ABH=tg ACH(ch-cgv)
=>HB=HC(tương ứng)
Vậy, HB=HC(DCCM)
bcó BC=6cm=>BH+CH=6cm
lại có BH=CH (theo câu a)
Do đó, BH+BH=6cm
hay 2BH=6cm => BH=3cm
Áp dụng định lý Py-ta-go vao tg ABH vuông tại H, ta có:
AH2+BH2=AB2
hay AH2=AB2-BH2
=>AH2=52-32
=>AH2=25-9
=>AH2=16
=>AH=4( vì AH>0)
Vậy AH=4cm
k cho mình nha, bài trình bày thế này 10 điểm 100% luôn
VN
14 tháng 3 2017
(Hương tự vẽ hình!)
a) Ta có \(\widehat{ABC}\)cân tại \(A\Rightarrow AH\)vừa là đường cao vừa là trung tuyến
\(\Rightarrow HB=HC\)
b) Ta có: \(HB=HC=\frac{BC}{2}=\frac{6}{2}=3\left(cm\right)\)
Xét \(\Delta ABH\)vuông tại \(H\)có:
\(AH^2+BH^2=AB^2\left(pytago\right)\)
\(AH^2+3^2=5^2\)
\(AH^2+9=25\Rightarrow AH^2=25-9=16\)
\(\Rightarrow AH=\sqrt{16}=4\left(cm\right)\)
4 tháng 7 2021
ABCHÁp dụng định lý Py - ta - Go vào tam giác ABC vuông tại A có :
AC2 = BC2 - AB2
AC2 = √52−32=3(AC>0)52−32=3(AC>0)
Ta có : SABC=12AB.ACSABC=12AB.AC
Mà : SABC=12AH.BCSABC=12AH.BC
⇒ 12AB.AC=12AH.BC12AB.AC=12AH.BC
⇔ AH = AB.ACBC=3.45=2,4(cm)
4 tháng 7 2021
ACBH
a) Áp dụng pi ta go ta có : AB2 = AH2 + BH2 = 162 + 252 = 881
=> AB = √881881
Lại có : BH.HC = AH2
<=> HC.25 = 162
<=> HC.25 = 256
<=> HC = 256 : 25 = 10,24
Ta có : BC = HC + BH = 10,24 + 25 = 35,24
Áp dụng bi ta go : AC2 = AH2 + HC2 = 162 + 10,242 = 360,8576
=> AC = √360,8576
CM
26 tháng 1 2017
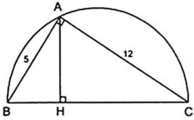
Áp dụng định lý Py – ta – go vào tam giác ABC vuông tại A ta có:
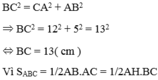
⇒ AH.BC = AB.AC
Hay 12.5 = AH.13 ⇒ AH = 60/13 ( cm )
Từ câu a ta có: Δ BHA ∼ Δ BAC ⇒ BH/BA = BA/BC hay BH/5 = 5/13 ⇔ BH = 25/13( cm )
Do đó: CH = BC - BH = 13 - 25/13 = 144/13( cm )
16 tháng 4 2022
a:Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=> \(BH=\dfrac{BC}{2}=3\left(cm\right)\)
nên AH=4(cm)
b: Ta có: AH là đường trung tuyến ứng với cạnh BC
mà G là trọng tâm của ΔABC
nên A,H,G thẳng hàng
c: XétΔABG và ΔACG có
AB=AC
AG chung
GB=GC
Do đó:ΔABG=ΔACG
Suy ra: \(\widehat{ABG}=\widehat{ACG}\)
Bạn tự vẽ hình nha!!!
AH là đường cao của tam giác ABC cân tại A
=> AH là đường trung trực của tam giác ABC.
=> H là trung điểm của BC
=> HB = HC = BC/2 = 6/2 = 3
Tam giác ABH vuông tại H có:
\(AB^2=AH^2+BH^2\) (định lí Pytago)
\(AH^2=AB^2-BH^2\)
\(AH^2=5^2-3^2\)
\(AH^2=25-9\)
\(AH^2=16\)
\(AH=\sqrt{16}\)
\(AH=4\)
BH=3cm
AH=4cm