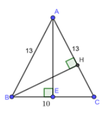
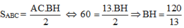Cho tam giác ABC có AB=AC=13cm;BC=10cm và M là trung điểm của cạnh BC.Từ M kẻ MH vuông góc với cạnh AB tại H và kẻ MK vuông góc với cạnh AC tại K.
a)tính độ dài đoạn thẳng AM
b)CM:AM là đường trung trực của đoạn thẳng HK
c)CM:BC song song vs HK
d)từ B kẻ BP vuông góc vs AC tại C.đoạn thẳng BP cắt đoạn thẳng MH tai I.CM:tam giác IBM cân