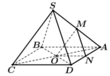
Câu 3: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P, Q lần lượt là trung điểm của BC, SB, SA, OP. a) Chứng minh mặt phẳng (OMN) song song với mặt phẳng (SCD). (0,5 điểm +vẽ hình 0,5 điểm) b) Chứng minh đường thẳng MQ song song với mặt phẳng (SCD). (0,5 điểm) Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi I là điểm thuộc AO, (P) là mặt phẳng đi qua I và song song với mặt phẳng (SBD). Xác định thiết diện của hình chóp cắt bởi mặt phẳng (P). ( 1,0 điểm)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1 : Trong sách
Ca 2 : Có 3 cách :
1. Chứng minh 2 đường thẳng đó đồng phẳng, rồi áp dụng phương pháp chứng minh song song trong hình học phẳng (như tính chất đường trung bình, định lí Talét đảo, …)
2. Chứng minh 2 đường thẳng đó cùng song song với đường thẳng thứ ba.
3. Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
Câu 3 :

Chà, bài này dựng xong hình là xong thôi (tính toán đơn giản bằng Talet)
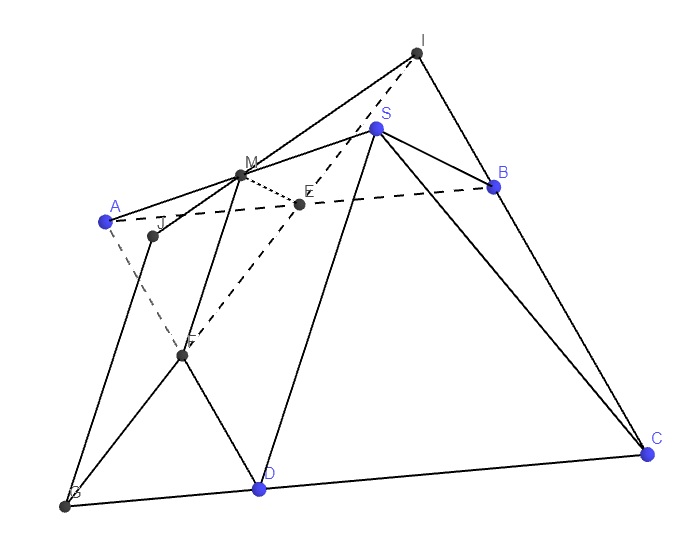
Đầu tiên là dựng mp qua M và song song (SBD): qua M kẻ các đường thẳng song song SB, SD lần lượt cắt AB, AD tại E và F
Nối EF kéo dài cắt BC tại I và CD tại G
Qua G kẻ đường thẳng song song MF (hoặc SD) cắt MI kéo dài tại J
Talet cho ta: \(\dfrac{MI}{MJ}=\dfrac{IF}{GF}\)
Mà \(\dfrac{GF}{GI}=\dfrac{DF}{BI}=\dfrac{\dfrac{1}{2}AD}{BC+\dfrac{1}{2}BC}=...\)
Vậy là xong

a) S là điểm chung của hai mặt phẳng (SAB) và (SCD) mà AB // CD
Từ S kẻ Sx sao cho Sx // AB // CD nên Sx là giao tuyến của hai mặt phẳng (SAB) và (SCD).
b) Gọi E là trung điểm của AB
G là trọng tâm tam giác SAB nên \(\frac{{EG}}{{SE}} = \frac{1}{3}\)
N là trọng tâm tam giác ABC nên\(\frac{{EN}}{{EC}} = \frac{1}{3}\)
Theo Ta lét, suy ra GN // SC mà SC \( \subset \) (SAC). Do đó, GN // (SAC)

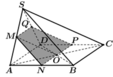
Tham khảo hình vẽ bên.
Gọi P, Q lần lượt là trung điểm của CD, SD. Khi đó thiết diện tạo bởi mặt phẳng (OMN) với hình chóp là hình thang MNPQ. Thật vậy:
![]()
Chọn B.

a: Xét ΔSAD có
M,N lần lượt là trung điểm của SA,SD
=>MN là đường trung bình của ΔSAD
=>MN//AD
Ta có: MN//AD
AD\(\subset\)(ABCD)
MN không nằm trong mp(ABCD)
Do đó: MN//(ABCD)
b: Xét ΔDSB có
O,N lần lượt là trung điểm của DB,DS
=>ON là đường trung bình của ΔDSB
=>ON//SB và \(ON=\dfrac{SB}{2}\)
Ta có: ON//SB
ON\(\subset\)(OMN)
SB không thuộc mp(OMN)
Do đó: SB//(OMN)
c: Xét ΔASC có
O,M lần lượt là trung điểm của AC,AS
=>OM là đường trung bình của ΔASC
=>OM//SC
Ta có: OM//SC
OM\(\subset\)(OMN)
SC không nằm trong mp(OMN)
Do đó: SC//(OMN)
Ta có: SB//(OMN)
SC//(OMN)
SB,SC cùng thuộc mp(SBC)
Do đó: (SBC)//(OMN)